算法学习
本文是算法分析的基础,提供时间复杂度分析所需的基础工具
算法思想复杂多样且在不断发展,学习算法要明确自己的目标。对我而言,能在工程代码中使用/分析常见算法即可,故本文并没有提供高深算法的介绍和讲解,仅仅包含简单算法的学习
参考 hello-algo,算法学习分三个阶段:入门、重复刷题(剑指 offer、LeetCode Hot 100 等)、构建体系
数学基础
数学归纳法(Mathematical induction, MI)和程序中的递归思想息息相关,也是很多算法证明与分析的基础,比如循环不变式和复杂度分析
循环不变式是一种条件,循环语句每执行一次循环就查看中间结果是否符合预想。为了使循环语句最终能够得到正确答案,这个条件必须保持不变(因此称为不变式),且必须成立
// 不变式必须在此处成立
while(...){
// 循环体
// 不变式在此处也必须成立
}
数学归纳法

一般地,证明一个与正整数 n 有关的命题,有如下步骤:
- 证明当 \(n\) 取第一个值 \(n_0\) 时命题成立,一般地取 \(n_0 =1\)
- 假设当 \(n = k( k≥n_0 ,k∈N^*)\) 时命题成立,证明当 \(n = k + 1\) 时命题也成立
上面证明过程的第二步是递推的依据,第一步是递推的基础
复杂度的渐进表示
细节可参考 wiki
| 符号 | 定义 |
|---|---|
| \(f(n)=O(g(n))\) | 渐近上限 |
| \(f(n)=o(g(n))\) | 渐近可忽略不计 (\(limit(f(n))/(g(n))=0\)) ,函数 g 的增长快于 f |
| \(f(n)=\Omega(g(n))\) | 渐近下限 (当且仅当 \(g(n)=O(f(n)) \)) |
| \(f(n)=\omega(g(n))\) | 渐近主导 (当且仅当 \(g(n)=o(f(n))\)) |
| \(f(n)=\Theta(g(n))\) | 渐近紧约束 (当且仅当 \(f(n)=O(g(n))\) 且 \(f(n)=\Omega(g(n)))\) |
常见时间复杂度
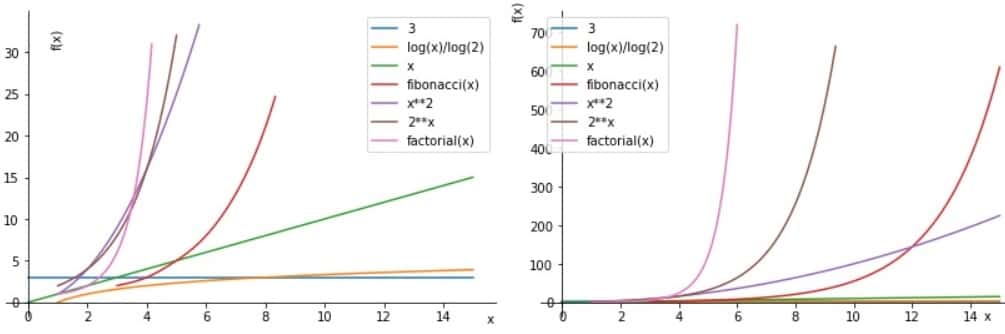
细节可参考 wiki 。常见时间复杂度如下所示:
- 多项式函数(\(O(n^d)\)):\(f(n)=a_{0}+a_{1} n+a_{2} n^{2}+\cdots+a_{d} n^{d}, a_d \neq 0\)
- 指数函数(\(O(r^n)\)):\(f(n)=r^n\)
- 阶乘函数(\(O(n!)\)):\(f(n)=n!\)
- 斯特林公式(Stirling’s formula):\(n !=\sqrt{2 \pi n}\left(\frac{n}{\mathrm{e}}\right)^{n}\left(1+\Theta\left(\frac{1}{n}\right)\right)\)
- 其他,略
递归树 & 主定理
主定理(Master theorem)提供了用渐近符号(大O符号)表示递推关系式的方法。在算法分析中可以使用主定理快速确定递归算法的时间复杂度,下面是简化版主定理,细节可以查看 wiki
形如 \(T(n)=a T\left(\left\lceil\frac{n}{b}\right\rceil\right)+O\left(n^{d}\right)\) 且 \(a>0, b>1, d \geq 0\) 那么可得:
\[T(n)= \begin{cases}O\left(n^{d}\right) & \text { if } d>\log _{b} a \\ O\left(n^{d} \log n\right) & \text { if } d=\log _{b} a \\ O\left(n^{\log _{b} a}\right) & \text { if } d<\log _{b} a\end{cases} \]
主定理的证明可以使用递归树,细节请参考递归式求解——代入法、递归树与主定理。使用递归树证明 \(T(n)=aT(n/b)+f(n)\) 的方式如下图所示:
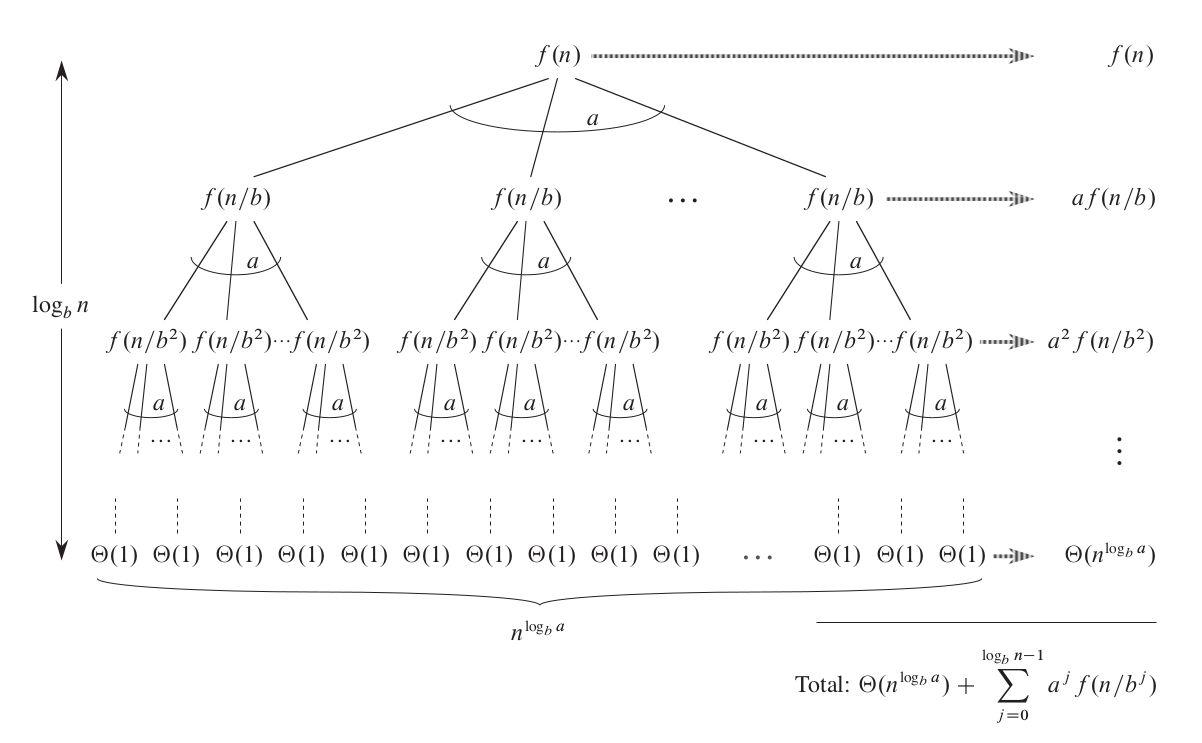
分析示例
二分查找是典型的分治算法,设二分查找时间复杂度为 \(T(n)\),那么可得 \(T(n) = T(n/2)+1\)(这里略去了奇数 \(n\) 的场景)。按主定理方式进行分析得 \(T(n)=O(log(n))\):
\[a=1,b=2\\ log_{b}a = log_2 1=0\\ log_2 n^0 = 0,d=0\\ d = log_b a\\ T(n)=O(n^0 log(n))=O(log(n)) \]
可以使用递归树分析进行验证,树高为 \(log(n)\),每层操作为 1。并不是所有的算法都可以使用主定理进行分析,例如下面的汉诺塔问题
# TowerOfHanoi(n,'A','B','C')
def TowerOfHanoi(n , source, destination, auxiliary):
if n == 1:
# move disk from A to B
return
TowerOfHanoi(n-1, source, auxiliary, destination)
TowerOfHanoi(n-1, auxiliary, destination, source)
汉诺塔递归代码如上,\(T(n)=2T(n-1)+1\)。使用迭代归纳法进行分析得 \(T(n)=O(2^n)\):
\[\begin{aligned} T(n) &=2 T(n-1)+1=2[2 T(n-2)+1]+1=2^{2} T(n-2)+2+1 \\ &=2^{2}[2 T(n-3)+1]+2+1=2^{3} T(n-3)+2^{2}+2+1 \\ &=\cdots \\ &=2^{n-1} T(1)+2^{n-2}+2^{n-3}+\cdots+2+1 \\ &=2^{n-1}+2^{n-2}+2^{n-3}+\cdots+2+1=2^{n}-1 \end{aligned} \]
\(m\) 元钱,投资 \(n\) 个项目。效益函数 \(f_i (x)\),表示第 \(i\) 个项目投 \(x\) 元的效益,\(i =1, 2, …, n\)。求如何分配每个项目的钱数使得总效益最大?
暴力法求解,可使用如下建模方式:
\[\underbrace{1 \ldots 1}_{x_{1} 个}0 \underbrace{1 \ldots 1}_{x_{2} 个}0 \ldots 0 \underbrace{1 \ldots 1}_{x_{n} 个} \]
时间复杂度如下式所示,\(m\) 个 1 和 \(n-1\) 个零组成一个数组时的组合数
\[C_{m+n-1}^{m}=\frac{(m+n-1) !}{m !(n-1) !}=\Omega\left((1+\varepsilon)^{m+n-1}\right) \]
基础数据结构
flowchart TB
A[数据结构]
C[数组、链表、<br/>栈、队列]
D[哈希表<br/>(链地址/开放地址)]
E[树]
subgraph Tree
E1[完美、完全、满、平衡]
click E1 "https://www.hello-algo.com/chapter_tree/binary_tree/"
E2[链表存储、数组存储]
E3[层序、先序、中序、后序遍历]
E4[平衡树:AVL、2-3、RB]
click E4 "https://www.hello-algo.com/chapter_tree/avl_tree/"
end
F[堆]
subgraph Heap
F1[大小顶堆、优先队列]
F2[基于数组]
F3[Top-K 问题]
end
G[图]
subgraph Graph
G1[有向、连通、有权]
G2[临接表<br/>邻接矩阵<br/>关联矩阵]
G3[BFS、DFS]
end
A --> C
A --> D
A --> E
A --> F
A --> G
E --> Tree
F --> Heap
G --> Graph
基础算法
- 递归、调用栈、尾递归
- 如果函数在返回前的最后一步才进行递归调用,则该函数可以被编译器或解释器优化,使其在空间效率上与迭代相当。这种情况被称为「尾递归 tail recursion」
- 其他