线代&矩阵

2018-11-16

12 min read

math

计算的目的不在于数字本身，而在于洞察其背后的意义 —— 理查德 - 哈明

参考资料： 3Blue1Brown / 《矩阵力量》 / 《PLAD》¹ / 《数值线性代数》 / LA for Coder /

常见概念

注：下表中的符号并不一定通用，不同资料中可能用不通的符号表示相同的计算，例如谱半径： \(\rho(A)\) 或 \(\sigma(A)\) 。更详细的矩阵特性汇总可以参考《The Matrix Cookbook》 / MATH1009.12 / ，矩阵微积分可以参考²

表达式	概念	备注
\(A^H\), \(A^T\)	埃米尔特 / 转置 /	实数 \(A\) ，则 \(A^H=A^T\)
\(A^*\)	伴随矩阵	1. 代数余子式 2. \(\mathbf{A}=\left[\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right]\)
\(Q^*=Q^{-1}\) , \(Q^HQ=I\)	酉（Unitary）矩阵	实数 \(Q\)，则 \(Q\) 正交；\(det(Q)=\pm1\)，刚性旋转或镜像
\(Gram(A)\)	格拉姆矩阵	\(A=[v_1,\cdots,v_n]\), \(G_{i j}=\left\langle v_i, v_j\right\rangle\)
\(\kappa(A)\)	条件数	条件数依赖于范数的选取（\(\left\\|A^{-1}\right\\|\cdot\\|A\\|\)）

矩阵的重点概念（备忘）：内存、速度、精度、扩展性、矩阵乘法、矩阵分解等
可以把矩阵（Matrix）相乘解读为对空间的变换（投影），\(AB\) 表示使用 \(A\) 对 \(B\) 做空间映射
可以从映射（投影）的角度考虑方程（\(Ax=b\)）解的个数。如果 A 满秩则映射前后 x 和 b 处于相同维度的空间，两者一一对应，故解唯一；如果 A 非满秩，则说明映射后 x 所处的空间被压缩（\(det(A)=0\)）。以三维变换（\(A\)）为例，A 非满秩，则 x 被压缩（投影）到平面或者点线，如果 A 代表的空间（xy 平面）和 b （z 方向）所处空间正交则无解；如果 b 属于 A 所在的空间，则有无穷多个处于更高维度的 x 可以被压缩（投影）到 b，此时方程的解无穷多

常见计算

张量积&联合 PMF

张量积（Tensor Product）又叫克罗内克积（Kronecker Product），两个列向量 a 和 b 张量积 \(a\otimes b\) 定义如下：

\[\boldsymbol{a} \otimes \boldsymbol{b}=\left[\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \end{array}\right]_{n \times 1} \otimes\left[\begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_m \end{array}\right]_{m \times 1}=\boldsymbol{a b}^{\mathrm{T}}=\left[\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \end{array}\right]\left[\begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_m \end{array}\right]^{\mathrm{T}}=\left[\begin{array}{cccc} a_1 b_1 & a_1 b_2 & \cdots & a_1 b_m \\ a_2 b_1 & a_2 b_2 & \cdots & a_2 b_m \\ \vdots & \vdots & \ddots & \vdots \\ a_n b_1 & a_n b_2 & \cdots & a_n b_m \end{array}\right]_{n \times m} \]

从几何视角，张量积与联合概率分布（Joint Probability Mass Function，\(\underbrace{p_{X, Y}(x, y)}_{\text {Joint }}=\underbrace{p_X(x)}_{\text {Marginal }} \cdot \underbrace{p_Y(y)}_{\text {Marginal }}\)）十分类似

\(L^p\) 范数&超椭圆

参考《矩阵力量》第三章

向量 \(x\) 的 \(L^p\)范数定义为：\(\|\boldsymbol{x}\|_p=\left(\left|x_1\right|^p+\left|x_2\right|^p+\cdots+\left|x_D\right|^p\right)^{1 / p}=\left(\sum_{j=1}^D\left|x_j\right|^p\right)^{1 / p}\)。给定列向量 \(\boldsymbol{x}=[x_1,x_2]^T\)

\(p\) 为 1 时，\(f(x_1, x_2)\) 函数的等高线为旋转正方形：\(f\left(x_1, x_2\right)=\left|x_1\right|+\left|x_2\right|\)，曼哈顿距离
\(p\) 为 2 时，\(f(x_1, x_2)\) 函数的等高线为正圆：\(f\left(x_1, x_2\right)=\sqrt{x_1^2+x_2^2}\)
\(p\) 为 \(+\infty\) 时，\(f(x_1, x_2)\) 函数的等高线为正方形：\(f\left(x_1, x_2\right)=\max \left(\left|x_1\right|,\left|x_2\right|\right)\)

克拉默法则

已知方程：\(\left\{\begin{array}{c}a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=b_1 \\ a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=b_2 \\ \cdots \cdots \cdots \cdots \cdots \\ a_{n 1} x_1+a_{n 2} x_2+\cdots+a_{n n} x_n=b_n\end{array}\right.\)。克拉默法则如下，其中 \(D_j(j=1,2, \cdots, n)\) 是把系数行列式 \(D\) 中第 \(j\) 列的元素用方程组右端的常数项代替后得到的 \(n\) 阶行列式。克拉默法则多几何解释可以参考 3Blue1Brow 或者知乎

\[\begin{aligned} &D=\left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right| \neq 0\\ &x_1=\frac{D_1}{D}, x_2=\frac{D_2}{D}, \cdots, x_n=\frac{D n}{D}, \end{aligned} \]

矩阵与线性变换（投影）

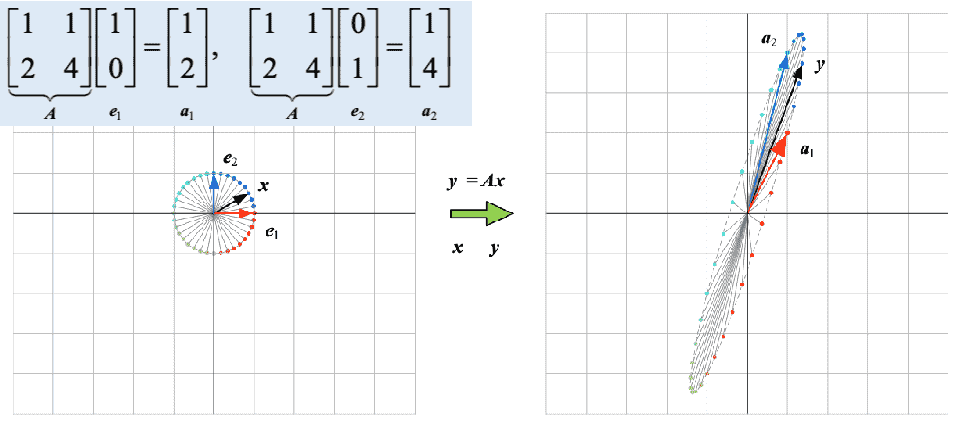
3Blue1Brown 对线性变换做了非常直观的介绍，可以从基变换的角度理解线性变换（\(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=x\left[\begin{array}{l} a \\ c \end{array}\right]+y\left[\begin{array}{l} b \\ d \end{array}\right]=\left[\begin{array}{l} a x+b y \\ c x+d y \end{array}\right]\)）。对于 \(Ax = b\)，通常把 \(A\) 当作一种变换（A 的列向量是新空间的基，如果 A 是单位矩阵，即基向量没变，则 \(Ax\) 变换结果不变），它通过乘法作用于向量 \(x\) 将其映射到另一个空间（同维或者异维），产生的新向量称为 \(Ax\) 。这种关于矩阵的观点（映射变换）是使用线性代数建立数学模型的关键。以内积为例，内积 \(u·v=\mid u\mid\mid v\mid cos(θ)\) 可以看作向量 \(u\) 在向量 \(v\) 方向上的投影长度乘向量 \(v\) 的模长，如下图所示。外积一般用于求两个向量平面的法向量

向量 u 在 v 方向上的投影结果为 z（上图，原点到虚线垂足），向量 z 的长度 (向量模) 就是 u 在 v 方向上的标量投影 (scalar projection)：\(s=\frac{u^{\mathrm{T}} v}{\|v\|}=\frac{v^{\mathrm{T}} u}{\|v\|}=\frac{u \cdot v}{\|v\|}=\frac{v \cdot u}{\|v\|}=\frac{\langle u, v\rangle}{\|v\|}\)

\[\boldsymbol{A}_{n \times D}=\left[\begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1, D} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, D} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, D} \end{array}\right], \quad \boldsymbol{B}_{D \times m}=\left[\begin{array}{cccc} b_{1,1} & b_{1,2} & \cdots & b_{1, m} \\ b_{2,1} & b_{2,2} & \cdots & b_{2, m} \\ \vdots & \vdots & \ddots & \vdots \\ b_{D, 1} & b_{D, 2} & \cdots & b_{D, m} \end{array}\right] \]

参考《矩阵力量》第六章（标量积展开 (scalar product expansion)），已知上面矩阵 A 和 B，\(AB\) 的结果可以看作 B 的每一列在 A 中每一行的投影。假设 B 只有一列（或以分块矩阵的视角，即以 B 的列 A 的行为主），那么得到的列向量，每个元素的值都是向量 B 在 A 对应行（行基）上的投影长度，示例如下

\[\boldsymbol{C}=\boldsymbol{A} \boldsymbol{B}=\left[\begin{array}{c} \boldsymbol{a}^{(1)} \\ \boldsymbol{a}^{(2)} \\ \vdots \\ \boldsymbol{a}^{(n)} \end{array}\right]_{n \times 1}\left[\begin{array}{llll} \boldsymbol{b}_1 & \boldsymbol{b}_2 & \cdots & \boldsymbol{b}_m \end{array}\right]_{1 \times m}=\left[\begin{array}{cccc} \boldsymbol{a}^{(1)} \boldsymbol{b}_1 & \boldsymbol{a}^{(1)} \boldsymbol{b}_2 & \cdots & \boldsymbol{a}^{(1)} \boldsymbol{b}_m \\ \boldsymbol{a}^{(2)} \boldsymbol{b}_1 & \boldsymbol{a}^{(2)} \boldsymbol{b}_2 & \cdots & \boldsymbol{a}^{(2)} \boldsymbol{b}_m \\ \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{a}^{(n)} \boldsymbol{b}_1 & \boldsymbol{a}^{(n)} \boldsymbol{b}_2 & \cdots & \boldsymbol{a}^{(n)} \boldsymbol{b}_m \end{array}\right]_{n \times m} \]

如下公式，从另一个角度（外积展开 (outer product expansion)）也就是以 B 的行和 A 的列为主来看，B 的每一行都被投影到以 A 列为基的新空间

\[\boldsymbol{C}=\boldsymbol{A} \boldsymbol{B}=\left[\begin{array}{llll} \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_D \end{array}\right]_{1 \times D}\left[\begin{array}{c} \boldsymbol{b}^{(1)} \\ \boldsymbol{b}^{(2)} \\ \vdots \\ \boldsymbol{b}^{(D)} \end{array}\right]_{D \times 1}=\boldsymbol{a}_1 \boldsymbol{b}^{(1)}+\boldsymbol{a}_2 \boldsymbol{b}^{(2)}+\cdots+\boldsymbol{a}_D \boldsymbol{b}^{(D)}=\sum_{i=1}^D \boldsymbol{a}_i \boldsymbol{b}^{(i)} \]

矩阵相乘可以看作变换的叠加，先旋转后剪切和先剪切后旋转的结果是不同的，所以矩阵相乘不满足交换律。可以将 \(AB\) 的结果看作拆分 \(B\) 的每一列和 \(A\) 做乘法（\(A x\)，\(x\) 是 \(B\)的某一列向量），最后将所有列整合的过程。那么 \(A\) 与 \(B\) 每一列的相乘（\(Ax_n\)）可以看作使用 \(B\) 的每一列对 \(A\) 做列的线性组合

如果使用坐标的形式记录图像在屏幕每个像素的位置，那么一个图就可以使用矩阵的形式进行保存，将图像矩阵与变换矩阵相乘，就可以得到变换后图像在屏幕中新的坐标信息。\(R^2\) 中的每个点 \((x,y)\) 都对应于 \(R^3\) 中的点 \((x,y,1)\) ，我们称 \((x,y)\) 有其次坐标 \((x,y,1)\) 。可以将左侧矩阵的每一列看作新坐标系的单位向量，就可以了解为什么下面的方式进行了平移操作

\[\left[\begin{array}{lll} 1 & 0 & h \\ 0 & 1 & k \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{c} x+h \\ y+k \\ 1 \end{array}\right] \]

旋转、镜像和伸缩

\[\left[\begin{array}{ccc} \cos \varphi & -\sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{array}\right], \quad\left[\begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right], \quad\left[\begin{array}{lll} s & 0 & 0 \\ 0 & t & 0 \\ 0 & 0 & 1 \end{array}\right] \]

常见矩阵分解

正交分解

The letter Q is often used to indicate orthogonal matrices

正交矩阵（\(\left\langle\mathbf{q}_i, \mathbf{q}_j\right\rangle= \begin{cases}0, & \text { if } i \neq j \\ 1, & \text { if } i=j\end{cases}\)）是方阵，且有一些十分特殊的性质，例如：\(\mathbf{Q}^{\mathrm{T}} \mathbf{Q}=\mathbf{I}\)，由此可得 \(Q^T\) 是 \(Q\) 的逆矩阵

Orthogonal vector decomposition involves breaking up a vector into the sum of two other vectors that are orthogonal and parallel to a reference vector

如上图所示，正交分解（向量）的基础是最短距离向量：\(\mathbf{a}^{\mathrm{T}}(\mathbf{b}-\beta \mathbf{a})=0\)，求解此方程可得：\(\beta=\frac{\mathbf{a}^{\mathrm{T}} \mathbf{b}}{\mathbf{a}^{\mathrm{T}} \mathbf{a}}\)。已知向量 \(t\) 和参考向量 \(r\)，可以得 \(t\) 的正交分解结果：

\[\begin{aligned} \mathbf{t}_{\| \mathbf{r}} & =\mathbf{r} \frac{\mathbf{t}^{\mathrm{T}} \mathbf{r}}{\mathbf{r}^{\mathrm{T}} \mathbf{r}} \\ \mathbf{t}_{\perp \mathbf{r}} & =\mathbf{t}-\mathbf{t}_{\| \mathbf{r}} \end{aligned} \]

矩阵的正交化（\(A=QR\)）就是将非正交矩阵（\(A\)，\(A\) 不一定是方阵）转换为正交矩阵（\(Q\)，\(Q\) 一定是方阵），常见的算法如斯密特正交化（Gram-Schmidt）。斯密特正交算法因为涉及了很多浮点计算，所以稳定性较差，Householder reflections 算法是比较稳定的正交化算法

从三维空间上看，相互正交的基向量组有无穷多，所以正交分解的结果并不唯一。使用 \(QR\) 分解求逆，相比于传统方法，更稳定。Householder reflections 是稳定的正交分解算法，随后求解 \(A^{-1}=(QR)^{-1}=R^{-1}Q^{-1}=R^{-1}Q^{T}\)，因为 \(R\) 是上三角矩阵，所以其逆求解起来相对数值稳定

LU & Cholesky 分解

\[A=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ * & 1 & 0 & 0 \\ * & * & 1 & 0 \\ * & * & * & 1 \end{array}\right]\left[\begin{array}{lllll} \mathbf{*} & * & * & * & * \\ 0 & \mathbf{*} & * & * & * \\ 0 & 0 & 0 & \mathbf{*} & * \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \]

将矩阵转化为下三角（Lower）和上三角（Upper）矩阵之积的形式即为矩阵的 LU 分解。因为 LU 分解后得到的是三角矩阵，所以求解方程会更加方便快速：\(Ax=L(Ux)=Ly={\bf b}\) ， \(Ly={\bf b}\) 和 \(Ux=y\)

对于一个 \(n\) 阶线性方程组（\(Ax=c\)），常规消元法求解矩阵方程的时间复杂度为 \(O(n^3)\)。虽然 LU 分解的时间复杂度也是 \(O(n^3)\) ，但解 \(Ly=b\) 和 \(Ux=y\) 的时间复杂度是 \(O^2\)。有大量不同的 \(c\) 需要求解 \(x\) ，那么 LU 分解后大量方程的求解时间复杂度将为 \(O(n^2)\)

Cholesky 分解把矩阵分解为一个下三角矩阵以及它的转置矩阵的乘积：\(\boldsymbol{A}=\boldsymbol{L} \boldsymbol{L}^{\mathrm{T}}\)，只有正定矩阵 (positive definite matrix) 才能 Cholesky 分解。对于正定矩阵，Cholesky 分解的数值稳定性和效率要比其他方法要高，细节可以参考这里

特征值分解

特征值分解（\(\mathbf{A} \mathbf{v}=\lambda \mathbf{v}\)）只适用于方阵，非方阵可以使用奇异值分解（SVD，Singular Value Decomposition）。从几何角度，特征向量在投影（\(A\)）前后方向不变（或反向），一般我们更关心特征向量的方向而非长度。特征值分解到用途有 PCA/噪声消除/数据有损压缩（如 jpg），都是去除特征值小的分量来减少数据量

满秩方阵减去特征值后得到的新方阵是奇异矩阵（singular）。由特征值分解方程可得 \((\mathbf{A}-\lambda \mathbf{I}) \mathbf{v}=\mathbf{0}\) ，已知 \(\mathbf{v}\) 非零，即方程 \((\mathbf{A}-\lambda \mathbf{I}) \mathbf{x}=\mathbf{0}\) 有除 \(\mathbf{x}=0\) 之外的解，这说明 \(\mathbf{A}-\lambda \mathbf{I}\) 的行列式为 0，即 \(\mathbf{A}-\lambda \mathbf{I}\) 为奇异矩阵。特征值的求解即利用行列式为 0 这个特性：\(|\mathbf{A}-\lambda \mathbf{I}|=0\)，获得特征值后求解线性方程组即可得对应的特征向量。M 维方阵有 M 个特征值和对应的特征向量

对角化&谱分析

对角化是将矩阵 A 以 \(\mathbf{V}^{-1} \boldsymbol{\Lambda} \mathbf{V}\) （旋转/缩放/旋转）的形式进行表达，其中 V 是 A 的特征向量、\(\boldsymbol{\Lambda}\) 是对应特征值构成的对角矩阵

\[\begin{aligned} \mathbf{A} \mathbf{V} & =\mathbf{V} \mathbf{\Lambda} \\ \mathbf{A} & =\mathbf{V} \mathbf{\Lambda} \mathbf{V}^{-1} \\ \mathbf{\Lambda} & =\mathbf{V}^{-1} \mathbf{A} \mathbf{V} \end{aligned} \]

如果 \(A\) 可以对角化，A 的 n 次幂可以写成：

\[\boldsymbol{A}^n=\boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1} \boldsymbol{V} \boldsymbol{D} \boldsymbol{V}^{-1}=\boldsymbol{V} \boldsymbol{D}^n \boldsymbol{V}^{-1}=\boldsymbol{V}\left[\begin{array}{llll} \left(\lambda_1\right)^n & & & \\ & \left(\lambda_2\right)^n & & \\ & & \ddots & \\ & & & \left(\lambda_D\right)^n \end{array}\right] \boldsymbol{V}^{-1} \]

如果 A 为对称矩阵，A 的特征值分解可以写成如下形式，其中 V 为正交矩阵。下式告诉我们为什么对称矩阵的特征分解又叫谱分解(spectral decomposition)，因为特征值分解将矩阵拆解成一系列特征值和特征向量张量积乘积之和，就好比将白光分解成光谱中各色光一样

\[\begin{aligned} \boldsymbol{A} & =\boldsymbol{V} \boldsymbol{\Lambda} \boldsymbol{V}^{\mathrm{T}}=\left[\begin{array}{llll} \boldsymbol{v}_1 & \boldsymbol{v}_2 & \cdots & \boldsymbol{v}_D \end{array}\right]\left[\begin{array}{llll} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & \lambda_D \end{array}\right]\left[\begin{array}{c} \boldsymbol{v}_1^{\mathrm{T}} \\ \boldsymbol{v}_2^{\mathrm{T}} \\ \vdots \\ \boldsymbol{v}_D{ }^{\mathrm{T}} \end{array}\right] \\ & =\lambda_1 \boldsymbol{v}_1 \boldsymbol{v}_1^{\mathrm{T}}+\lambda_2 \boldsymbol{v}_2 \boldsymbol{v}_2{ }^{\mathrm{T}}+\cdots \lambda_D \boldsymbol{v}_D \boldsymbol{v}_D{ }^{\mathrm{T}}=\sum_{j=1}^D \lambda_j \boldsymbol{v}_j \boldsymbol{v}_j{ }^{\mathrm{T}} \\ & =\lambda_1 \boldsymbol{v}_1 \otimes \boldsymbol{v}_1+\lambda_2 \boldsymbol{v}_2 \otimes \boldsymbol{v}_2+\cdots \lambda_D \boldsymbol{v}_D \otimes \boldsymbol{v}_D=\sum_{j=1}^D \lambda_j \boldsymbol{v}_j \otimes \boldsymbol{v}_j \end{aligned} \]

幂迭代法

\[b_{k+1}=\frac{A b_k}{\left\|A b_k\right\|} \]

幂迭代法（Power Iteration）可以用于求解有单最大特征值矩阵最大特征值对应的特征向量，迭代过程如上公式。这里需要确定 \(A\) 的一个特征值比其他特征值都大，\(b_0\) 是不为 0 的随机向量

二次型与正定

矩阵 A 的二次型形如 \(\mathbf{w}^{\mathrm{T}} \mathbf{A} \mathbf{w}=\alpha\) ，其中 \(\alpha\) 是实数 \(\mathbf{w}\) 是列向量，\(\alpha\) 的正负描述了矩阵 \(A\) 的正定性（Definiteness）。实正定矩阵对称

\[\begin{array}{llll} \hline \text { Category } & \text { Quadratic form } & \text { Eigenvalues } & \text { Invertible } \\ \hline \text { Positive definite } & \text { Positive } & + & \text { Yes } \\ \text { Positive semidefinite } & \text { Nonnegative } & + \text { and } 0 & \text { No } \\ \text { Indefinite } & \text { Positive and negative } & + \text { and }- & \text { Depends } \\ \text { Negative semidefinite } & \text { Nonpositive } & - \text { and } 0 & \text { No } \\ \text { Negative definite } & \text { Negative } & - & \text { Yes } \\ \hline \end{array} \]

矩阵 A 的正定性可以从其特征值的正负和特征向量的线性组合角度理解，如上表所述。从几何的角度，一个矩阵是正定的，可以认为经过 A 投影后的向量 \(\mathbf{A}\mathbf{v}\) 和原向量 \(\mathbf{v}\) 方向相同，或着可以认为 A 的基向量和原始向量空间的基向量大致同向。细节可以参考《PLAD》第 13 章

\[\left[\begin{array}{ll} x & y \end{array}\right]\left[\begin{array}{ll} 2 & 4 \\ 0 & 3 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=2 x^2+(0+4) x y+3 y^2 \]

以二阶矩阵为例，不同正定负定情况下其三维图形如下

奇异值分解

设 A 是实 \(m \times n\) 矩阵，则必存在正交矩阵（\(\mathbf{U}^{\mathrm{T}} \mathbf{U}=\mathbf{I}, \ \mathbf{V}^{\mathrm{T}} \mathbf{V}=\mathbf{I}\)） \(\boldsymbol{U}=\left[\boldsymbol{u}_1, \cdots, \boldsymbol{u}_m\right] \in \mathbb{R}^{m \times m}\) 和 \(\boldsymbol{V}=\left[\boldsymbol{v}_1, \cdots, \boldsymbol{v}_n\right] \in \mathbb{R}^{n \times n}\) ，使得 \(\boldsymbol{U}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{V}=\operatorname{diag}\left(\sigma, \cdots, \sigma_{\boldsymbol{p}}\right) \in \mathbb{R}^{m \times n}\) 其中 \(\boldsymbol{p}=\min \{m, n\}\)，\(\sigma_1 \geqslant \sigma_2 \geqslant \cdots \geqslant \sigma_p \geqslant 0\)

可以将 SVD（Singular Value Decomposition）看作特征值分解的泛化，\(A=\left(\begin{array}{ccc}3 & 2 & 2 \\ 2 & 3 & -2\end{array}\right)\) SVD 示例如下：

\[A=U \Sigma V^T=\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 / \sqrt{2} & -1 / \sqrt{2} \end{array}\right)\left(\begin{array}{lll} 5 & 0 & 0 \\ 0 & 3 & 0 \end{array}\right)\left(\begin{array}{rrr} 1 / \sqrt{2} & 1 / \sqrt{2} & 0 \\ 1 / \sqrt{18} & -1 / \sqrt{18} & 4 / \sqrt{18} \\ 2 / 3 & -2 / 3 & -1 / 3 \end{array}\right) \]

奇异值分解有一些特性，例如特征值矩阵中的值从大到小排列，特征值总是非复的，且都是实数（即使原始矩阵中有复数）。非 0 奇异值的个数与矩阵的秩相等

应用示例

皮尔逊&余弦相关性

向量的点乘表示一个向量在另一个向量上的投影长度，如果将所有向量归一化，然后求解向量点乘，即可获得向量之间的相关性。皮尔逊（\(\rho=\frac{\widetilde{\mathbf{x}}^{\mathrm{T}} \widetilde{\mathbf{y}}}{\|\widetilde{\mathbf{x}}\|\|\widetilde{\mathbf{y}}\|}\)）相关性使用 mean val 归一化向量，然后获得两个向量 \([-1, 1]\) 的相关性数值

余弦相关性（\(\cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}\)）考虑两个向量之间的夹角，夹角越小，相关性越大。皮尔逊和余弦相关性公式类似，但结果并不完全相同。细节可以参考《PLAD》第四章

def corrAndCosine(x,y):
  num = np.dot(x,y) 
  den = np.linalg.norm(x) * np.linalg.norm(y) 
  cos = num / den   # 余弦相关性

  xm  = x-np.mean(x)
  ym  = y-np.mean(y)
  num = np.dot(xm,ym)
  den = np.linalg.norm(xm) * np.linalg.norm(ym) 
  cor = num / den   # 皮尔逊相关性
  return cor,cos

滤波&特征检测

对于时间序列，使用不同时长的滤波片段（kernel）可以提取（过滤）不同频率的波形特征。细节可以参考《PLAD》第四章

Cohen, Mike X. Practical Linear Algebra for Data Science. " O’Reilly Media, Inc.", 2022. ↩︎
Hu, Pili. “Matrix calculus: Derivation and simple application.” City University of Hong Kong, Tech. Rep (2012). ↩︎