数字电路基础-原理与方法

2022-03-16

9 min read

techs

数字设计层次

数字设计从底向上可以分为：物理级（渗杂等） / 晶体管级别（MOS 实现门电路） / 逻辑设计（74 模块） / HDL

不同层级的设计有各自的好处，《数字设计：原理与实践》1.13 节给出了一个例子：相同的模块，设计层级越高，一般所需要的晶体管越多，但有些模块（如多路复用器）直接使用晶体管级别的设计会更好，这是 HDL 综合时进行优化的一个方向

数制与编码

二进制补码

二进制系统中只实现加法器即可实现二进制数的加法和减法，以四位二进制为例，如上图所示。加法即顺时针移动指针，减法则逆时针移动指针，减法的逆时针也可以使用顺时针移动实现，顺时针移动量由 \(C-n+1\) 确定。以 4 位二进制数为例，C 为 16，n 为负数的绝对值。也可以从另一个角度来理解二进制补码（\(B 2 T_{w}\)，Binary to Two’s-complement 的缩写，长度为 \(w\) ）：

\[\begin{aligned} &B 2 T_{4}([0001])=-0 \cdot 2^{3}+0 \cdot 2^{2}+0 \cdot 2^{1}+1 \cdot 2^{0}=0+0+0+1=1 \\ &B 2 T_{4}([0101])=-0 \cdot 2^{3}+1 \cdot 2^{2}+0 \cdot 2^{1}+1 \cdot 2^{0}=0+4+0+1=5 \\ &B 2 T_{4}([1011])=-1 \cdot 2^{3}+0 \cdot 2^{2}+1 \cdot 2^{1}+1 \cdot 2^{0}=-8+0+2+1=-5 \\ &B 2 T_{4}[[1111])=-1 \cdot 2^{3}+1 \cdot 2^{2}+1 \cdot 2^{1}+1 \cdot 2^{0}=-8+4+2+1=-1 \end{aligned} \]

格雷码

格雷码是一个二进制数系，其中两个相邻数的二进制位只有一位不同，格雷码的顺序并不唯一（结合 n 维体可证明）。格雷码可以减少误差，例如这里举的位置示例。格雷码的构造方式有多种，比较常见的有镜像法和直接构造法，细节参考这里或者leetcode ，使用整数直接生成格雷码的代码如下：

// 生成 n 位二进制的一种格雷码序列
vector<int> grayCode(int n) {
    vector<int> ret(1 << n);
    
    for (size_t i = 0, size = ret.size(); i < size; ++i) {
        ret[i] = (i >> 1) ^ i;
    }
    return ret;
}

上面代码的证明分为两种情况（自己举几个例子就明白了）：

整数 n 二进制最右侧二进制位为 0，则 n+1 和 n 在二进制表示上只有最右侧一位不同，满足格雷码的要求
整数 n 二进制最右侧二进制位为 1，则 n+1 和 n 在二进制表示上至少有两位不同。举例子可明白上面的原理

n 维体

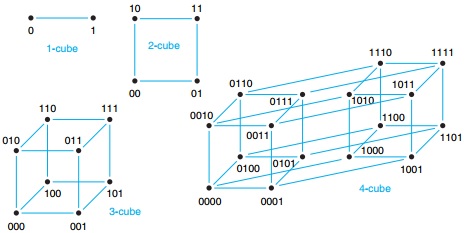
n 维体有 \(2^n\) 个顶点，每个顶点用一个 n 位二进制串标记。画几何图的边时，令每个顶点与另外 m 个顶点相邻，而这 m 个顶点的位串与给定的顶点只有一位不同

设计 n 位格雷码的问题等效于沿着 n 维体的边寻找一个路径，路径上每个顶点恰好被访问一次，从这个角度可以看出格雷码的顺序并不唯一。汉明码中编码距离是 n 维体中两点之间的最短距离

霍夫曼编码

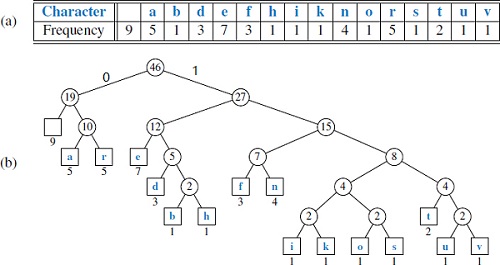
霍夫曼编码可以按照信息出现的概论使用不同长度的编码对信息进行编码，出现概率大的信息使用短的编码，细节可以参考这里。霍夫曼树是属于前缀树，任何一个编码都不是另一个编码的前缀。这就保证了编码被解码时不会有多义性

开关（布尔）代数

公理&定理

一个数学系统的公理（axiom，或假设（ postulate））是假定其值为真的基本定义的最小集，由此可推导出关于系统的所有其他信息。开关代数的公理\单变量定理、二变量定理和三变量定理这里就不再重复

对偶性&德摩根

对偶性原理：对开关代数的任何定理或恒等式，若交换所有的 0 和 1 以及 “ +” 和 “ • ”，结果仍正确

德摩根定理（De Morgan’s laws）是与/或运算转换的基础，使用对偶性原理可以非常方便的证明德摩根定理

\[AB=C \\ (A'+B')=C'\\ (A'+B')'=C\\ AB=(A'+B')'\\ \]

可以使用韦恩图证明德摩根定理，细节请参考这里或者这里

下面是广义德摩根定理：

\[\left[\mathrm{F}\left(\mathrm{X}_{1}, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n},+, \cdot\right)\right]^{\prime}=\mathrm{F}\left(\mathrm{X}_{1}^{\prime}, \mathrm{X}_{2}^{\prime}, \cdots, \mathrm{X}_{n}^{\prime}, \cdot,+\right) \]

广义德摩根示例如下：

\[\begin{aligned} \mathrm{F}(\mathrm{W}, \mathrm{X}, \mathrm{Y}, \mathrm{Z}) &=\left(\mathrm{W}^{\prime} \cdot \mathrm{X}\right)+(\mathrm{X} \cdot \mathrm{Y})+\left(\mathrm{W} \cdot\left(\mathrm{X}^{\prime}+\mathrm{Z}^{\prime}\right)\right) \\ &=\left((\mathrm{W})^{\prime} \cdot \mathrm{X}\right)+(\mathrm{X} \cdot \mathrm{Y})+\left(\mathrm{W} \cdot\left((\mathrm{X})^{\prime}+(\mathrm{Z})^{\prime}\right)\right) \\ {[\mathrm{F}(\mathrm{W}, \mathrm{X}, \mathrm{Y}, \mathrm{Z})]^{\prime} } &=\left(\mathrm{W}+\mathrm{X}^{\prime}\right) \cdot\left(\mathrm{X}^{\prime}+\mathrm{Y}^{\prime}\right) \cdot\left(\mathrm{W}^{\prime}+(\mathrm{X} \cdot \mathrm{Z})\right) \end{aligned} \]

香侬展开定理

\[\begin{aligned} &\mathrm{F}\left(\mathrm{X}_{1}, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n}\right)=\mathrm{X}_{1} \cdot \mathrm{F}\left(1, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n}\right)+\mathrm{X}_{1}^{\prime} \cdot \mathrm{F}\left(0, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n}\right) \\ &\mathrm{F}\left(\mathrm{X}_{1}, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n}\right)=\left[\mathrm{X}_{1}+\mathrm{F}\left(0, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n}\right)\right] \cdot\left[\mathrm{X}_{1}^{\prime}+\mathrm{F}\left(1, \mathrm{X}_{2}, \cdots, \mathrm{X}_{n}\right)\right] \end{aligned} \]

在用 FPGA 实现组合逻辑函数的应用中，香侬展开定理非常重要。FPGA 包含了一个被称为査询表（LUT）的基本资源的许多实例，LUT 可以实现任何组合逻辑功能，但是，其输人有一个固定的上限，大约是 4~6 个。如果需要一个 7 输入的函数，怎么办呢？香农定理说明了如何将几个 4~6 输入 LUT 的输出组合起来，实现任何 7 输入的逻辑函数，依次类推，复杂的组合逻辑都可以使用基本的 LUT 实现

逻辑函数的标准表示法

Max/Min Term

逻辑函数最基本的表示法是真值表（truth table），其他形式还有逻辑表达式、波形图和 HDL 描述。下面给出一些后面用到的定义

字面值（literal）是一个变量或变量的补，例如：X、Y、Y'
标准项（normal term）是一个乘积项或求和项，其中每个变量只出现一次
n 变量最小项（minterm）是具有 n 个字面值的标准乘积项。共有 \(2^n\) 个这样的乘积项。最小项的值和对应真值表中的输出值是没有关系的，这也是最小项被称为 on-set 的原因，最小项性质如下：
1. 在输入变量任一取值下，有且仅有一个最小项取值为 1（即取值落在真值表的某一行）
- 全体最小项之和为 1；任何两个最小项之积为 0
- 两个相邻（只有一项不同，类似格雷码）的最小项之和可以合并，消去一对因子，只留下公共因子。这个特点是使用卡诺图化简逻辑表达式的基础，也是下面 QM 算法的基础
n 变量最大项（maxterm）是具有 n 个字面值的标准求和项。共有 \(2^n\) 个这样的求和项

真值表和最大项、最小项之间有紧密的联想。下面是最大项和最小项的一个示例

\[\begin{array}{ccccccc} \text { Row } & \mathrm{X} & \mathrm{Y} & \mathrm{Z} & \mathrm{F} & \text { Minterm } & \text { Maxterm } \\ \hline 0 & 0 & 0 & 0 & \mathrm{~F}(0,0,0) & \mathrm{X}^{\prime} \cdot \mathrm{Y}^{\prime} \cdot \mathrm{Z}^{\prime} & \mathrm{X}+\mathrm{Y}+\mathrm{Z} \\ 1 & 0 & 0 & 1 & \mathrm{~F}(0,0,1) & \mathrm{X}^{\prime} \cdot \mathrm{Y}^{\prime} \cdot \mathrm{Z} & \mathrm{X}+\mathrm{Y}+\mathrm{Z}^{\prime} \\ 2 & 0 & 1 & 0 & \mathrm{~F}(0,1,0) & \mathrm{X}^{\prime} \cdot \mathrm{Y} \cdot \mathrm{Z}^{\prime} & \mathrm{X}+\mathrm{Y}^{\prime}+\mathrm{Z} \\ 3 & 0 & 1 & 1 & \mathrm{~F}(0,1,1) & \mathrm{X}^{\prime} \cdot \mathrm{Y} \cdot \mathrm{Z} & \mathrm{X}+\mathrm{Y}^{\prime}+\mathrm{Z}^{\prime} \\ 4 & 1 & 0 & 0 & \mathrm{~F}(1,0,0) & \mathrm{X} \cdot \mathrm{Y}^{\prime} \cdot \mathrm{Z}^{\prime} & \mathrm{X}^{\prime}+\mathrm{Y}+\mathrm{Z} \\ 5 & 1 & 0 & 1 & \mathrm{~F}(1,0,1) & \mathrm{X} \cdot \mathrm{Y}^{\prime} \cdot \mathrm{Z} & \mathrm{X}^{\prime}+\mathrm{Y}^{\prime}+\mathrm{Z}^{\prime} \\ 6 & 1 & 1 & 0 & \mathrm{~F}(1,1,0) & \mathrm{X} \cdot \mathrm{Y} \cdot \mathrm{Z}^{\prime} & \mathrm{X}^{\prime}+\mathrm{Y}^{\prime}+\mathrm{Z}^{\prime} \\ 7 & 1 & 1 & 1 & \mathrm{~F}(1,1,1) & \mathrm{X} \cdot \mathrm{Y} \cdot \mathrm{Z} & \mathrm{X}^{\prime}+\mathrm{Y}^{\prime}+\mathrm{Z}^{\prime} \\ \hline \hline \end{array} \]

真值表的逻辑可以使用最大项（闭集，off-set）和最小项（开集，on-set）直接表示：

PLD

使用真值表得到最大/最小项逻辑表达式后可以进行化简，化简后的逻辑表达式一般只有三种操作：与、或、非，这正是 PLD 的基本组件，通过烧录来确定器件之间的连接方式即可使用 PLD 实现对应的逻辑。下图描述了 PLD 的大致实现与使用方法

HDL

上面逻辑使用 HDL 进行描述，结果如下

// on set, minterm
case ({X,Y,Z})
    0,3,4,6,7: F = 1;
    default:   F = 0;
endcase

// off set, maxterm
case ({X,Y,Z})
    1,2,5:   F = 0;
    default: F = 1;
endcase

组合电路的分析与综合

组合逻辑电路可以使用真值表和逻辑表达式进行分析。真值表分析的复杂度和输入位数成指数级关系，所以逻辑表达式更为常用。很多工具提供了逻辑表达式的化简与优化，例如 Python 中 Sympy 库中的 Logic 模块。如下图所示，复杂电路化简后可以用一个异或门表示

综合与电路化简

综合指代从所需功能的准确形式定义开始到构建出具体实现（一个能够实现这个功能的物理逻辑电路）的过程。在不同工艺下不同门电路有着不同的性能，CMOS 场景下与非门和或非门要比常见的与门和非门要快，但对于设计而言我们常使用与门与或门（因为直观）

电路最小化

为减少片上逻辑占用，组合电路最小化技术非常重要

卡诺图

以 \(2^{n}\) 个小方块分别代表 \(n\) 变量的所有最小项，并将它们排列成矩阵, 而且使几何位置相邻的两个最小项在逻辑上也是相邻的（只有一个变量不同）, 就得到表示 \(n\) 变量全部最小项的卡诺图

输入位数不大（一般小于 6）的场景可以使用卡诺图来化简组合电路，取值为 1 的变量用原变量表示，取值为 0 的变量用反变量表示，出现不同值的变量直接消除，示例如下：

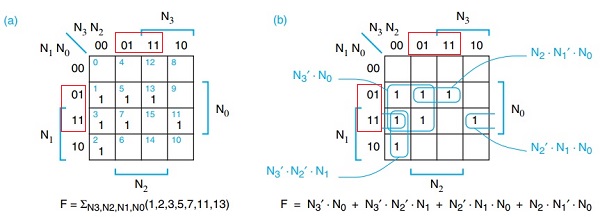
卡诺图的化简可以使用约束项和任意项，不过约束项与任意项和电路使用场景相关

约束项：逻辑函数中对输入变量的取值有限制，与这些被限制的取值对应的最小项称为约束项
任意项：在输入变量某些取值下，函数值为1或0不影响逻辑电路功能，与这些取值对应的最小项称为任意项
无关项：约束项和任意项统称为无关项，它们可以写入逻辑式，也可以不写入逻辑式

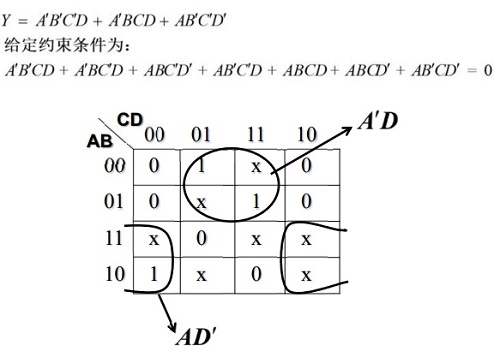
QM 算法

卡诺图适合较少的输入逻辑，输入位数过大后卡诺图就不那么直观且卡诺图化简难以使用代码实现。奎因－麦克拉斯基算法（Quine-McCluskey）在功能上等同于卡诺图但方便使用程序实现。QM 算法的运行时间随输入大小而呈指数增长（\(3^n/n\) ）

竞争&冒险

同时反向的逻辑电平变化称为竞争(Race)。由于电路延迟，逻辑电路的瞬态特性可能与稳态分析得到的不同。特别是，在稳态分析下的不变的输出可能会产生短脉冲，常常称为尖峰或闪烁。若电路可能产生尖峰，就说它存在冒险（hazard）。冒险分静态冒险和动态冒险

任何电路都可以进行冒险分析，实现无冒险电路比较困难，不过也只有在少部分场景下才需要无冒险电路。电路的冒险分析可以使用逻辑方法、电路图法与卡诺图法进行分析，细节请参考其他书籍，下面给出几个例子

有形如 \(Y = AA'\) 形式的表达式，有竞争
卡诺图中相切的“圆”有竞争。消除的方法是用新的圆把相切的部分包含起来，使用“冗余”电路消除竞争

状态机

The state of a sequential circuit is a collection of state variables whose values at any one time contain all the information about the past necessary to account for the circuit’s future behavior.

如果知道当前风扇转速的 “状态”，就可以确定风扇转速控制电路当前的输出了。风扇转速是现态，对于一个三速风扇而言，这个现态可以存储为一个 2 位二进制状态变量，这种 2 位二进制状态变量分别代表十进制数 0 到 3，0 对应着 off 状态，而 3 对应着最高风扇转速状态。给定现态（风扇转速 0 ~ 3 ），就可以把下一个状态作为输入（即上 / 下按动按钮）的函数，从而预测出下一个状态。当然，我们需要更多的状态变量来描述时序电路的操作——一个电路在任意给定的状态下会对一个给定的输人做出怎样的反应

上面的风扇是一个简单的例子，可以从风扇的输出（即转速）来判断电路的状态，且很容易判断下一个状态。但一些场景下仅仅用输出并不能判断电路的状态且无法判断下一个状态。以交通灯为例，十字路口的交通灯在换向的时候有一个所有灯全红的间隔，也有一个所有灯闪烁的状态。某一个时刻所有灯为红，我们并不能确定控制灯的状态是处于全红间隔还是闪烁状态。我们也不能通过全红的信号灯来判断信号灯的下一个状态。为了解决这类问题，电路使用不同的编码表示不同的状态（不同方向转向后的双红和闪烁使用不同的编码），不同的编码可以对应着相同的输出

有限状态机

具有 n 位二进制状态变量的电路就有 \(2^n\) 种可能的状态。尽管是一个很大的数目，但它总归有限，绝不可能是无限的。所以，有时也将时序电路称为有限状态机（Finite State Machines, FSMs），更常简称为状态机（state machine）。无限状态机是有数学模型的（如图灵机），它们一般包括一个小的有限状态机控制单元，以及海量辅助存储器（如磁带）。大多数时序电路的状态变化所发生的时间是由一个自运行的时钟（clock）信号来规定的

状态机电路大致可以分为两大类，Mealy 型和 Moore 型，二者结构如下图所示。二者的区别在于输出是否和现态输入有关

状态机器的分析可以使用转移方程、状态转移表、状态转移图等工具