STA-延时计算

芯片上比较常用的延时有¹：

1. 传播延时（最大延时），\(t_{pd}\) 表示从输入越过 50% 至输出越过 50% 之间的最长时间
2. 污染延时（最小延时），\(t_{cd}\) 表示从输入越过 50% 至输出越过 50% 之间的最短时间
3. 上升/下降时间，\(t_r/t_f\) 表示波形从稳定值的 20% 至 80% 所需时间
4. 边沿速率，\(t_{rf} = (t_r +t_f)/2\)

我们可以从不同角度来提升影响系统工作速度的关键路径，微结构、逻辑级、电路与版图。良好的微结构能产生最大的影响

延迟计算

微分方程

计算电路延时的方式有多种，例如使用微分方程可以建立电路的物理模型并求得其瞬态响应。使用微分方程描述晶体管时常使用晶体管的长沟道模型。随着芯片制程的发展，长沟道模型已经不适用先进制程下的晶体管，使用微分方程精确刻画晶体管行为变得困难。先进工艺下的晶体管很多特性是非线性的，使用微分方程为这些晶体管建模很多时候难以求得闭式解。使用数值法求解这类方程并不能给出更深刻的涵义，所以真实的延迟求解器常使用其他模型

RC 模型

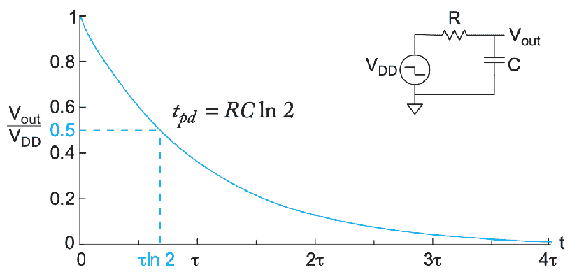
RC 延时模型采用在逻辑门翻转区间上的平均电阻和电容来近似非线性晶体管的 I-V 和 C-V 特性。这一近似虽然在详细预测模拟行为方面有明显的局限性，但它却能非常好地估计延时

简单的 RC 电路（如上图所示¹），通过频域模型（\(H(s)=\frac{1}{1+s R C}\)）可求的 \(V_{out}\) 时域模型：\(V_{\text {out }}(t)=V_{D D} \mathrm{e}^{-t / \tau}\)。由 RC 求得的时间常数 \(\tau\) 可以用于计算 RC 延迟。因为标准延迟求的是 \(V_{out}/V_{DD}=0.5\) 时的时间，而时间常数求的是 \(V_{out}/V_{DD}=e^{-1}=0.367879...\) 时的时间，标准延迟约是 RC 时间常数的 70% （\(ln(2)=0.69314718...\)）

Elmore

一般来说，我们所关心的大多数电路都可以表示成一个 RC Tree，即一个没有闭合回路的 RC 电路。这一树结构的根就是电压源，而叶子就是在各条支路末端的电容。Elmore 延时模型把从信号源发生翻转到其中一个叶子节点发生变化之间的延时估计为将在每个节点 \(i\) 上的电容 \(C_i\) 乘以从信号源至该节点及该叶子节点间公共路径的等效电阻的积全部相加所得到的和：\(t_{p d}=ln2*\sum_i R_{i s} C_i\)，示例如上图。一些场景下 \(R\) 已经包含了系数 \(ln2\)，所以表达式可以直接写成：\(t_{p d}=\sum_i R_{i s} C_i\)

65nm 或者稍微旧一点的工艺，互联线延迟没有那么显著。此时的门延迟包含两个部分：寄生延时( paiasidc delay)和努力延时( effort delay)。寄生延时是一个门驱动它自己内部扩散电容所需要的时间。加大晶体管的宽度将减小电阻但会增大电容，因此寄生延时在理想上与门的尺寸无关。努力延时取决于外部负载电容与输入电容的比，因而它随晶体管的宽度而变。 它也取决于门的复杂程度

线性延迟模型

线性延迟模型常使用两部分进行描述：寄生延迟和单级努力

一个门的逻辑努力定义为这个门的输入电容与一个能提供与这个门相同输出电流的反相器的输人电容之比。换言之，逻辑努力表示当一个门的每一个输人端只能表现出与反相器有相同的输人电容时，它在产生输出电流方面比起反相器来有多差

一个门的寄生延时是当这个门驱动零负载时的延时，它可以用 RC 延时模型来估算

互联线延迟

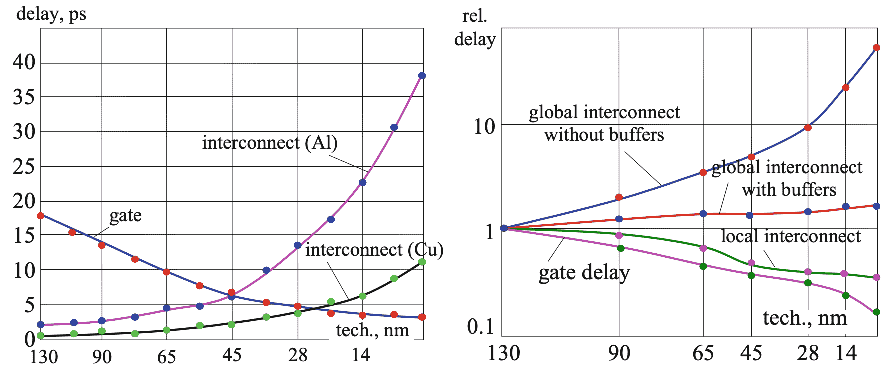
在 VLSI 的早期阶段，晶体管较慢。导线较宽较厚因而具有很低的电阻。在这些情形下，可以将导线看成是具有集总电容的理想等电位节点。但在现代 VLSI 工艺下，晶体管的翻转要快得多²。同时导线也变得更窄，这使它们的电阻迅速加大，因此在许多信号路径中导线的 RC 延时已超过了门延时

电阻&电容

现在的集成电路一般有 10 层或者更多的金属互联层¹。最上面的金属层一般用于分布电源和时钟，因为其具有最低的电阻。65nm 工艺下长 1mm 宽 0.125um 厚 0.22um 的铜导线电阻大概为 800 欧。接触孔或者通孔电阻大概在 2～20 欧。一个较大尺寸的门电路，其延迟会受到互联线明显的影响

—条导线是一个具有单位长度电阻和电容的分布电路（PEEC），它的行为可以用多个集总元件近似。三种标准的近似是 L 模型、\(\pi\) 模型和 T 模型。L 模型是较差的选择，因为它需要大量的小段才能得到精确的结果。 \(\pi\) 模型三段就足以给出精确到 3% 的结果

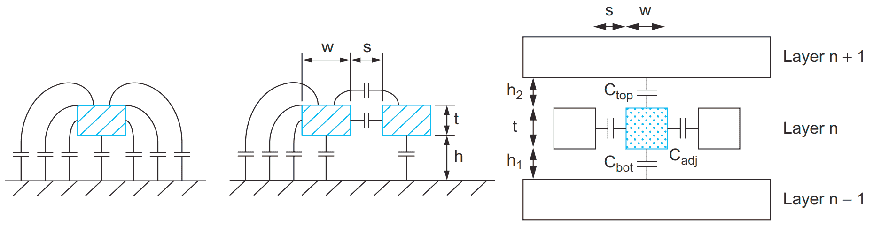
互联线的电容分为多个个部分：衬底电容、边缘电容和耦合电容等。电容的计算相比于电阻而言要复杂一些，不同场景下使用不同的电容模型。更精确的电容计算需要更大的计算量，三维模型会提供比二维模型更精确的结果。可以使用一些常见的工具来提取电容，例如 FastCap 或者 HSPICE

互联线特性

电感与趋肤效用都会影响到互联线到延迟，这里不做过多介绍。随着集成密度的提高，互联线之间容性和感性串扰对系统的影响也在不断提高。负载电容包括在总电容内，所以对于较短的导线和较大的负载，负载电容将占支配地位因而串扰的影响不大。反之，串扰对长导线的影响就非常大。如果一条导线和它相邻的导线都发生翻转，那么翻转的方向将影响必须传送的电荷数量及翻转的延时

芯片内的互连线大致可以分为三种：短线、中长线、长线。短线，即局部互连线，短线主要用于逻辑门之间或者用于速度不是很高的器件间的连接；中长线，即模块间互连线，中长线信号传输的速度要求比短线高，电感耦合效应也变得突出，因而容易引起很高的噪声；长线，即全局互连线，长线对电路性能起着关键作用，长线特别需要采用低电阻率金属以减小信号线和电源线的电阻损耗，需要厚的绝缘层来增加特征阻抗、减小延时，需要较宽的线间距以减少串扰。虽然宽线、宽间距可以减小RC延时和串扰，但也会影响布线密度

互连线的几何尺寸和拓扑结构会对互连线的电容、电阻、电感产生影响，从而影响互连线延时、功耗和可靠性。因此，需要建立用于分析互连线的实际特性和参数间关系的电气模型。目前，常见的互连线模型有以下几种

1. 集总 C 模型。只考虑电容，计算简单，但纳米级别工艺下精度不够
2. 集总 RC 模型。导线长度超过若干微米后电阻效应就会比较明显，此时需要考虑电阻和电容。集总 RC 模型在信号波长短时精度也较低，Elmore 延时较 SPICE 模型计算偏差大于 33%
3. 分布式 RC 模型。分布式 RC 模型有三种，L，\(\pi\) 和 T，如上图所示，其中 \(\pi\) 模型效果最好
4. 传输线模型，即 RLC 模型。RLC 模型精度高，但计算量也大

Wireload Models

在 RTL 代码综合阶段进行静态时序分析时，由于互连线还没有物理信息，因此可以通过调用线负载模型来估算实际物理实现后的线负载大小，用于静态时序分析时计算互连线延时。线载模型通过输出端口的负载个数估算负载电阻和电容

标准单元延迟

标准单元库（Standard Cell Library）是计算时序信息的必要组件，其中包含了计算时序约束所需要的各类参数，例如 Setup&Hold time、delay、power 和 Area 等。标准单元库有多种描述格式，本文以 Liberty 为主。Liberty 文件示例可参考其他资料，大部分模型，例如 NLDM、CCS 等都可以使用 Liberty 进行描述。Liberty 文件的介绍可以参考刘峰《静态时序分析》第四章

线性模型

线性模型（\(D=D 0+D 1 * S+D 2 * C\)，S/C 表示 input slew 和 load cap，Dx 由拟合算法获取）因为不能很好的刻画 Cell 大部分特性，所以较少使用

\[\begin{aligned} & t_{\mathrm{d}}=\left(k_1+k_2 C_{\mathrm{L}}\right) t_{\mathrm{t}}+k_3 C_{\mathrm{L}}^3+k_4 C_{\mathrm{L}}+k_5 \\ & t_{\mathrm{f}}=\left(k_1^{\prime}+k_2^{\prime} C_{\mathrm{L}}\right) t_{\mathrm{t}}+k_3^{\prime} C_{\mathrm{L}}^2+k_4^{\prime} C_{\mathrm{L}}+k_5^{\prime} \end{aligned} \]

当单元负载是纯电容时，还可以用线性方程来求解延时（如上公式，K-Factor），该方程以输人信号斜率 \(t_t\) 和输出负载 \(C_L\) 为变量，\(t_d/t_f/k_i\) 分别为单元门延时、输出信号斜率和方程常系数

非线性模型

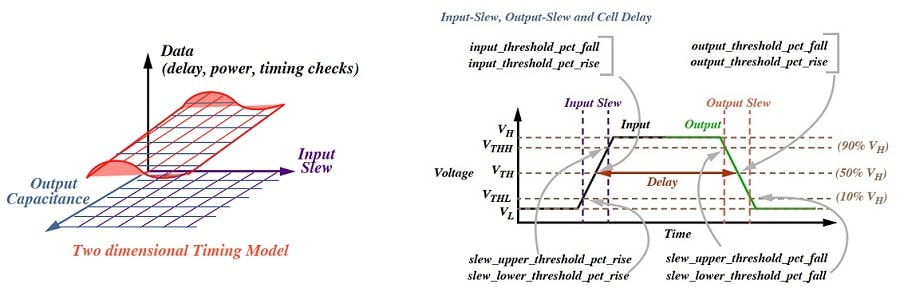
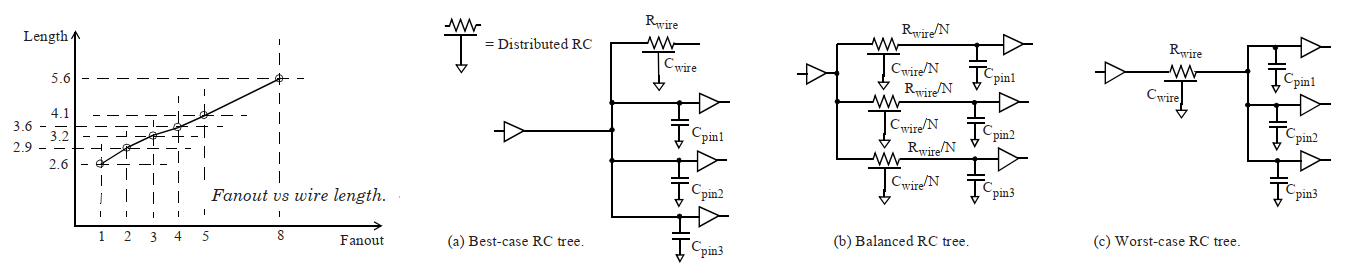
非先进制程，对于一个组合逻辑电路单元，其特性可以使用输入信号和输出负载进行刻画。为简化计算与分析过程，输入信号取跳变时间（Slew），输出负载取等效电容，如此电路单元的各种特性均可以使用二元函数进行描述（如上图所示）这种简化的描述电路特性的方式被称为 Two dimensional Timing Model。更复杂的电路可以使用多维模型进行建模，如 CCS。为减少计算量，多维信息常使用 LUT（Look Up Table）进行保存。二维 LUT 可以用来记录单元的 Delay、Output slew、Power 和时序检测（setup/hold 等）等信息

NLDM&SPDM

在 0.13um 工艺及以上时，互连线电阻远小于驱动电阻，逻辑门的输出波形基本可以通过戴维南等效电压源的计算结果来精确表达

使用二维时序模型，标准单元的延迟信息可以使用跳变时间（slew）和有效负载电容进行描述。因为非线性模型（NLDM，Non-Linear Delay Model）相比于线性模型效果要好，所以 NLDM 更为常用。上升沿和下降沿电路的组成可能不同（例如 Output high/low drive 不同），所以上升沿和下降沿信息要分别考虑

可伸缩多项式模型 SPDM 采用一组多项式参数去模拟延时数据。它解决了电压和温度变化的问题，并有效地弥补了 NLDM 的一些缺陷， 提高了精确性。但在实际应用中，由于很难提供所要求的变量及其相应的参数供 SPDM 去做模拟，这就使得它的应用受到了一定的限制

CCS/ECSM

如下图所示，先进制程下输出负载值在某个时间点由于密勒效应的影响发生了突变，基于单一负载值的输出波形无法精确反映该状态，因此需要更复杂的时序模型，例如 CCS/ECSM

ECSM/CCS 是根据实际制造好的晶体管参数而建立的物理模型，可以处理时序、功耗、噪声等。 它和 SPDM —致的是都去模拟硅片中的纳米效应，而与传统模型 SPDM 相比，ECSM 不依赖于其他数学模型，依据电流源模型去做简洁的标定，它能更加有效地跟踪晶体管在髙负载情况下的非线性电流开关特性。一些细节可以参考³

延迟优化

电路延迟主要受四个方面影响

1. 模块结构，可以类比软件结构
2. 逻辑级别，电路子模块的选型
3. 电路级别，单元类别与尺寸
4. 版图级，不同模块在芯片上的位置与距离会直接影响互联线延迟，同时影响串扰与噪声
   1. 由于电阻和电容都随导线长度增加而增长，所以一条导线的 RC 延时随 \(l^2\) 增长。为了减小延时可以将导线划分成 N 段并插人称为中继器的反相器或缓冲器来有效驱动导线
   2. 减少互联线之间串扰的方法也有多种：增大线距、屏蔽导线、确保相邻线在不同的时间上翻转、抵消串扰等

在电路设计的不同阶段 STA 计算延迟的模型也不一样。时序分析中逻辑门延时（Cell Delay）和信号线延时（Interconnect Delay）这两个参数值组成的阶段延时（stage delay）是时序分析中计算延时的主要组成部分

串扰与噪声

深微米以及纳米技术中串扰（Crosstalk）和噪声（Noise）会深刻影响电路与信号完整性（signal integrity）的设计与分析⁴。降低耦合的方式有多种，例如屏蔽（Shielding）、增加线距（Wire spacing）、Fast slew rate、Deep n-well、Isolating a block 等

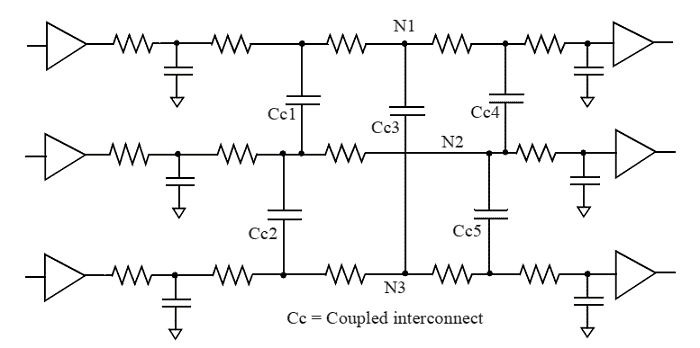
Broadly, there are two types of noise effects caused by crosstalk glitch, which refers to noise caused on a steady victim signal due to coupling of switching activity of neighboring aggressors, and change in timing (crosstalk delta delay), caused by coupling of switching activity of the victim with the switching activity of the aggressors

信号毛刺

Net 信号的跳变会造成相邻 Net 的容性毛刺（Glitch）从而影响信号完整性⁴。Glitch 的振幅受多重因素影响，例如耦合电容的大小、Net 信号跳变的幅度与速度、Victim 网络自身电容的大小和负载大小等因素。Glitch 有四种：Rise and Fall Glitches、Overshoot and Undershoot Glitches

串扰延迟

数字芯片上 Net 的电容会受相邻 Net 的影响，如果当前 Net 所有相邻 Net 的电压值是固定的，则当前 Net 与其他 Net 的耦合电容可以认为是固定值。然而如果相邻 Net 的电压也在不断的变化，那当前 Net 与其他 Net 的耦合电容也将是变化的，例如相位相反时耦合电容值大，相位相同时耦合电容值小

与 Glitch 类似，为了降低累计 delay 的值，crosstalk delay 的分析也包含了时间窗口和功能分类等方法