初识数学
本文是阅读 《数学简史》 / 《数学:确定性的丧失》 / 《数学基础》 / 等书籍的读书笔记
Mathematics is the queen of science, and arithmetic the queen of mathematics. – Carl Friedrich Gauss
数学的起源
数学源自生活,比如计数。由于人类的每只手有 5 个手指,每只脚有 5 个脚趾,五进制一度得到了广泛的应用,至今某些南美洲部落仍用手计数:1,2,3,4,手,手和1,等等;12也常被用作数基,这可能与它能被 6 个数整除有关,也可能是因为一年有 12 个朔望月;二十进制也曾被广泛使用,它使我们想起人类的赤脚时代,一双手和一双脚共 20 个指头,美洲印第安人使用过它,其中包括高度发达的玛雅文明;十进制被广泛采纳,是由于我们绝大多数人生来具有 10 个手指。还有大量其他进制的计数方式出现在人类的历史中,这些计数方式也多源自生活
古埃及有着比较发达的几何数学,这是因为他们需要使用几何知识来测量与分配位于尼罗河周边的农田和建造金字塔。当古埃及人开始使用几何时因为可用知识太少,难免犯错,例如公元前 1650 年《莱因德数学纸草书》记载的求解四边形面积的公式:\(S=\frac {(a+b)(c+d)} 4\),这个公式只对矩形有效。巴比伦使用 60 进制,因为观星的需要,古巴比伦在代数领域有着丰富的经验,他们对勾股定理的发现比东西方早了千年,例如早于公元前 1600 年的普林顿 322 号泥板
随着社会的发展,为了描述与使用新的技术与现象,新的数学被不断的发明出来
数学的“不确定性”
我们从小就被灌输数学不会出错的思想,然而这是不对的。时代的发展伴随着新思想对老思想的替换,我们不能说过去的知识不正确,只能说过去的知识可能不适用于当下。工业革命时期牛顿力学几乎是所有科学的基础,相对论的出现说明牛顿力学只是在一定尺度内是正确的。虽然相对论证明牛顿力学并非“真理”,但现实生活中的大部分场景下它足够精确且初等物理中牛顿力学依旧是重点
毕达哥拉斯学派认为万物皆数,宇宙是以数学方式设计的,借助数学知识我们可以充分认识它。这种思想和两千年后拉普拉斯决定论的思想类似。然而今天,随着混沌理论和信息理论的发展(包括哥德尔不完备定理),我们确信无法使用有限的数学公理精确描述这个无穷的宇宙
柏拉图认为这个世界是数学的,我们只能从理想世界的数学知识来理解这个世界的实在性和可知性。亚里士多德是柏拉图的学生,然而他和他的老师有着相反的看法,他认为物质的东西是实在的主体的源泉,物理学和一般的科学必需研究现实世界并从中获得真理,真正的知识是从感性的经验通过直观和抽象而获得的,这种抽象不能独立于人的思维而存在。随后的两千多年里,柏拉图和亚里士多德的思想不断影响着数学和物理的发展
伽利略主张废除物理的解释,只求数学的描述。伽利略的这一主张部分反对亚里士多德的观点,但伽利略认为物理的基本原理应该源于经验和实验,这是对亚里士多德观点的部分支持。这为后来牛顿创建万有引力提供了理论基础(只求数学描述而不求物理解释),终牛顿一生他都没有找到万有引力的自然科学解释,晚年他认为万有引力听从上帝的指挥。这里多说一句,牛顿创建万有引力不是为了科学,而是为了证明上帝是以数学的方式创建了这个世界,他要证明神对这个世界的控制无处不在。牛顿是虔诚的基督徒,对宗教的兴趣是他从事数学和科学研究的真正动力
牛顿是 17 世纪伟大的数学和物理学家,他的伟大在于使用他的万有引力解释了前人的理论。牛顿三定律在牛顿之前已经存在,只是没有人统一这些理论。牛顿和莱布尼兹一同开创了微积分,然而牛顿和莱布尼兹都无法解释他们在微积分中所使用的无穷小到底是个什么“东西”。分析数学(微积分)的基础要等到百年之后极限与集合论的创建。这百年间,分析数学一直在“裸奔”,因为没有人能证明微积分是正确的,虽然它已经应用于社会和科学领域的方方面面
其他人们无法理解但长时间使用的数学工具是负数和复数,\(\sqrt {-1} = i\) 是17/18 世纪很多数学家和工程师无法理解的,然而在解代数方程和工程问题时他们还是在使用这些工具。负数和复数在那时还不像自然数那么直观,直到高斯引入复平面,大家才慢慢理解复数的概念
随着时代的发展,神学慢慢从物理和数学的世界中淡化,人们不再相信万能的上帝创建了这个世界…
“无穷的磨难”
A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it —— Max Planck
就如普朗克所言一个新的科学真理并不是靠说服它的对手并使其看见真理之光取胜,而是由于它的对手死了,新的一代熟悉它的人成长起来了,数学的发展伴随着重重阻力。当代大部分数学的基础是集合论,然而集合论的奠基人却不受当时时代的理解。康托尔是集合论的奠基人,它提出了一一对应法来比较无穷集的大小并对其进行分类,如下图所示(细节可参考《从一到无穷大》),但被当时的人们认为是异端邪说,他自己也死在了精神病院。与无穷相关的故事有很多,比较经典的是希尔伯特旅馆

东西方的数学
东西方对数学的发展都做出了极大的贡献。古代东方以经验为依据的方法,在回答“如何” 这个问题时,是自信满满的,但当回答更为科学的追问“为什么” 时,就不那么胸有成竹了。西方数学起源于希腊,希腊数学有两个显著的特点,一是抽象化和演绎精神,二是它与哲学的关系非常密切,西方数学在回答“为什么”的方向上走的更远,推动了逻辑的发展
从东西方两本经典数学教材可以看出东西方对数学的不同看法。西方经典的数学书籍是《几何原本》,《原本》使用几条公理(axiom)或者称为假设(postulate)推导并证明了一系列的定理,如下面介绍的勾股定理和 \(\sqrt 2\) 不是有理数的证明;《九章》总结了中国当时常见的几百个问题并给出了解决办法,但没有说明为什么要那样做
为什么东西方看待数学的方式如此不同?有一种说法认为是地理环境和政治因素造成的…
游牧出身的希腊人有着勇于开拓的精神,他们不愿意因袭传统,更喜欢接触并学习新鲜的事物。希腊城邦始终处于割据状态,这当然与它的地理因素有关,山脉和海洋把人们分散在遥远的海岸上。希腊的社会主要由贵族和平民组成,二者并未完全割裂,战争时二者由国王领导,而国王只是某个贵族的首领。如此,这个社会便容易产生民主和唯理主义氛围
春秋战国时期百家争鸣,中国数学成就斐然。汉武帝独尊儒术后,名、墨著作中的数学论证思想失去进一步发展的机会
综观包括中世纪在内的古代中国数学史,数学家们大多是在以八股文取得一定的功名之后,才开始从事自己喜欢的数学研究。他们没有希腊的亚历山大大学和图书馆那样的群体研究机构和资料信息中心,只能以文养理或以官养理。学者们总是首先致力于统治阶级要求解决的问题。在中国古代,数学的重要性主要通过它与历法的关系显现出来,后者因为与信仰有关而成为帝王牢牢掌控的一个特权。最杰出的数学头脑总是围绕着那几个古老的计算问题,他们普遍缺乏开辟新天地的勇气和胆量。而希腊有些数学家已经开始为了数学而探索数学
经典证明
勾股定理
《几何原本》中对勾股定理的证明比较繁琐,这里展示了一个较简单的证明方式:
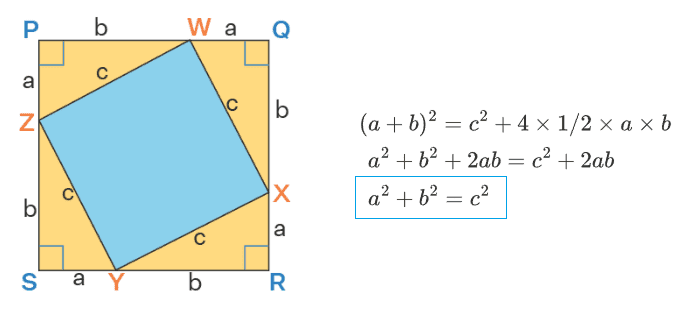
\(\sqrt 2\) 是无理数
证明过程如下:
- 假设 \(\sqrt{2}\) 是有理数,那么可假设 \(\sqrt{2}=\frac{n}{m}\),\(n\) 和 \(m\) 已经化简,其中必然有一个奇数
- \(\left(\frac{n}{m}\right)^{2}=2 \quad \rightarrow n^{2}=2 m^{2}\),因为 \(n^2\) 是偶数,所以 \(n\) 是偶数。两个奇数之积依然是奇数
- 因为 \(n\) 是偶数所以 \(n^2\) 可以被 4 整除,\(m^2=n^2/2\) 是偶数,\(m\) 是偶数
- 上面得到 \(m\) 和 \(n\) 都是偶数的结论,与上面二者至少一个奇数相悖,所以 \(\sqrt 2\) 是无理数
- 证毕
逻辑合理吗?
希腊数学基于公理,使用公理证明定理,从而解释“为什么”,公理和定理的定义如下,细节可以参考 wiki
- 公理:在传统逻辑中,公理是没有经过证明,但被当作不证自明的一个命题。通常公理都很简单,且符合直觉
- 定理:经过受逻辑限制的证明为真的陈述
公理通常很简单,且符合直觉。直觉一定正确吗?苏格兰哲学家休谟(D.Hume, 1711—1776)认为知觉的产生是不可理解的,我们不知道他来自外部事务、心灵深处还是上帝。不正确的直觉造成了错误的公理,那以错误公理为基础的逻辑大厦还稳固吗?
1739 年,休谟在一本著作中否定了宇宙中的事物遵循一定的法则。他的不可知论表明,科学是纯粹经验性的,欧几里得几何定理未必是真理。休谟否认了自然法则的必然性、永恒性和不可破坏性
事实上,欧几里得几何并非无懈可击,从它诞生之日起,就有一个问题困扰着数学家们,那就是第五公设,也称平行公设。它的叙述不像其他 4 条公设那样简单明了,当时就有人怀疑它不像一个公设而更像一个定理。这条被达朗贝尔戏称为“几何学的家丑”的著名公设是这样叙述的:
如果一条直线与两条直线相交(如下图所示),使得一侧的内角不都是直角,则如果将这两条直线延长,它们在内角不都是直角的直线一侧相交

上面这条共设没有想象中那么直观,数学家用了两千多年的时间也没有找到合适的公设取代这第五公设。当然,也没有人在欧氏几何中证明或者证伪这条公设
既然第五公设不好用,那换掉他不就好了。很多数学家使用不同的公设取代了第五公设(例如过平面外一点可以有多条直线与已知直线平行),从而创建与直觉相悖但自洽的全新的几何领域,例如黎曼几何。黎曼几何是相对论的数学基础,一个与直觉相悖的公设居然也是可用的…
另一个与直觉相悖的数学是哈密尔顿提出的四元数,四元数与现今的矩阵计算类似,不支持代数中的交换律,即 \(AB \neq BA\)。但它也是正确可用的…
现在我们可以下结论了:
数学中没有真理,即作为现实世界普世法则意义上的真理。希腊人试图从几条自明的真理出发仅仅使用演绎的证明方法来保证数学的真实性被证明是徒劳的
即使如此,我们也不应该悲观,数学依旧有其不可替代的功能。数学公理和定理不一定是物理世界的真理,某些领域的经验启发的特定公理,在这些领域内依旧可以非常精确的做有价值的描述。只是这些领域一旦扩展,这种适应性就可能失去,可能需要引入新的公理或者修改已有公理
创建数学的基础
从 19 世纪后半页开始,无数数学家为了夯实数学的基础而不懈的努力:希尔伯特、罗素、策梅罗、皮亚诺、彭加勒等伟大的数学家。在创建数学基础的过程中出现了各大数学流派
- 逻辑主义,代表人物罗素、怀特海。逻辑主义要把数学奠定在逻辑的基础上,不需要任何数学公理,数学不过时逻辑的主题和规律的自然延申
- 直觉主义,代表人物克罗内克、魏尔。直觉主义通过唤醒人们内心确认的约束以实来寻求数学真理。他们认为从逻辑推理出来的东西不比直接感悟的更可信。直觉主义否认排中律的正确性,哥德尔不完备定理也否决了排中律的正确性:在指定的理论框架内,有些命题无法证明也无法证伪
- 形式主义,代表人物希尔伯特。形式主义认为数学思想的要素是符号和由符号组合或串联而成的命题,这和程序很相似。形式主义后来发展出了元数学,希尔伯特希望使用元数学统一所有数学问题。当然,后来我们知道这是不可能的
- 集合论公理化,代表人物策梅罗。策梅洛-弗兰克尔集合论(Zermelo-Fraenkel Set Theory),含选择公理时常简写为 ZFC,是在数学基础中最常用形式的公理化集合论,不含选择公理的则简写为 ZF。它是二十世纪早期为了建构一个不会导致类似罗素悖论的矛盾的集合理论所提出的一个公理系统
虽然大部分创建数学基础的努力以失败告终,但这些数学流派对数学的发展有着不可磨灭的贡献,部分进展也促进了其他领域的发展
地基的崩塌

就像一座建筑,其晃动会随着高度增加而愈加明显,而在其上随意添加东西则更加危险。古希腊人不仅看到了这种危险,而且也进行了必要的重建。他们采用了两种方法。头一种方法是选一块坚实的地面,大厦就建在其上,这块坚实地面就是关于空间和正整数的自明真理。第二种方法是把钢筋加入框架之中,这些铜筋就是数学大厦结构中每一部分的演绎证明
当数学大厦的上层建筑得以加强之时,其基础——希措人所选定的公理却开始塌陷。非欧几何的发明揭示出欧几里得几何公理并非真正坚实的土地,只不过在表面看起来似乎坚实,非欧几何的公理也是如此
虽然数学事实上已经失去其基础,数学却又一次度过了难关。不幸的是,这种新结构的基础所用的水泥并没有很好地固化,建造者并不保证其坚固性
哥德尔不完备定理的提出与证明彻底否决了人们构造大一统数学基础的可能性,哥德尔定理的描述如下:
- 任何自洽的形式系统,只要蕴涵皮亚诺算术公理,就可以在其中构造在体系中不能被证明的真命题,因此通过推理演绎不能得到所有真命题(即体系是不完备的)
- 任何逻辑自洽的形式系统,只要蕴涵皮亚诺算术公理,它就不能用于证明其本身的自洽性
我们可以从信息论的角度来描述哥德尔不完备定理(可参考《信息简史》)。信息量使用比特进行度量,无论如何压缩,一张图片都不能能被压缩成 0 比特。任何极限压缩后压缩文件的大小都可以用来描述原文件包含的信息量。这个世界是混沌的,包含的信息量无穷多,所以无法被压缩成固定大小的文件块。数学公理哪怕有百万千万条,其中包含的信息量依旧是有限的,因为我们可以用有限大小的硬盘空间来保存描述这些公理的文字。使用有限信息量的公理来描述无限信息量的宇宙,这是不可能的,所以创建大一统的数学公理体系也是不可能的
另一个理解哥德尔不完备定理的角度是图灵机和可计算性。\(\pi\) 是可计算数,我们可以使用pi 的莱布尼兹公式无限逼近 \(\pi\) 值,而且这个过程可以编码实现。大部分有理数都是可计算的。蔡廷常数是不可计算数,这说明有些命题是无法证明的。细节可参考《信息简史》或者《图灵的秘密:他的生平、思想及论文解读》
ZFC 集论(暂略)
策梅洛-弗兰克尔集合论(Zermelo-Fraenkel Set Theory),含选择公理时常简写为 ZFC,是在数学基础中最常用形式的公理化集合论,不含选择公理的则简写为 ZF。它是二十世纪早期为了建构一个不会导致类似罗素悖论的矛盾的集合理论所提出的一个公理系统