读《大数据——互联网大规模数据挖掘与分布式处理》
常见概念
-
数据挖掘的定义与意义
- 定义:数据挖掘是数据模型的发现过程
- 模型的含义:统计建模(高斯分布等)/机器学习(贝叶斯网络/SVM/决策树等)/数据汇总(PageRank)/特征抽取(频繁项/相似项,例如协同过滤)
-
在大数据领域常使用非精确(统计)方法实现快速的计算
- 非精确过滤器:布隆过滤器;非精确 DV 计数:HyperLogLog
-
邦弗朗尼原理
-
二级存储器,主存之外计算机可以访问的所有数据存储器
-
TF.IDF(Term Frequency & Inverse Document Frequency,词频 & 逆文档频率),用于描述词语在文档中的重要性,钟形结构。\(w_{i, j}=t f_{i, j} \times \log \left(\frac{N}{d f_{i}}\right), for\ a\ term\ i\ in\ doc\ j\)
-
Modulus 运算桶数选择素数的原因
- 如果大部分原始数据与桶值有公约数,那么普通的模运算将造成大部分数据分布不均匀,比如所有的 key 都是偶数且槽点个数为偶数,那么奇数槽位将不会有值。使用素数可以减少这类情况
-
使用 hash 创建索引
- 将待查询的数据以某个字段为准取 hash 值并将其位置写入到对应的 hash 桶中;查找时将数据转化为 hash 并找到对应的桶。这个过程一次性过滤了大量的数据
-
自然底数 e 的来源与用途
- \(\lim _{N \rightarrow \infty}\left(1-\frac{1}{N}\right)^{N} \rightarrow \frac{1}{e} \approx 0.367879\) ,\(e\approx 2.718281828 \)
- 使用重抽样技术即可得自然底数 e 的值,参考
-
幂律
- 幂定律,简称幂律,即两个变量在对数空间下呈现出线性关系(\(\log y=b+a \log x\))。一般用马太效应解释幂律现象。常见的幂律现象如:PageRank 节点的度/Web 网站的大小/齐夫定律(Zipf)
MapReduce
MapReduce 一般由多个 Map 任务、主控制器和多个 Reduce 任务组成,各自的职能如下
- Map 任务将文件转化为 key/value 序列,同一个 Map 任务会给每一个 Reduce 任务生成一个临时文件保存这些序列
- 主控制器使用 hash 等算法将 Map 任务生成的 key/value 按照 key(可以是普通的字符串也可以是元组)进行分组与合并,相同的 key 交予相同的 Reduce 进行处理。主控合并来自不同 Map 任务但 key 相同的数据时会生成键-值表序列,例如:\(\left(k,\left[v_{1}, v_{2}, \cdots, v_{n}\right]\right)\)
- Reduce 任务每次处理一个键,并将与当前键相关的所有值以某种方式组合起来
- reducer,一般将 Reduce 作用在一个 key 上的过程称为一个 reducer,按照 MapReduce 的特性,一个 reducer 会处理一个全局 unique 的 key
- 当 Reduce 任务满足交换与结合律时可以将 Reduce 的部分任务放入 Map 中
- 因为每个 Map 任务会为每个 Reduce 任务生成一个临时文件,故 Reduce 任务的个数不能太多
MapReduce 的应用
矩阵与向量的乘积
已知矩阵 \(M\) 和列向量 \(v\),\(Mv\) 的元素 \(x_i\) 可由如下公式描述:\(x_{i}=\sum_{j=1}^{n} m_{i j} \nu_{j}\)
- Map 任务用于生成如下 key/value 序列:\(\left(i, m_{i j} v_{j}\right)\)
- Reduce 任务求每一个 \(key = i\) 值表中所有元素之和即为 \(x_i\)
如果列向量特别大,很难置入内存中,一般的处理方法:
- 将矩阵与向量切分为条,存入到不同的机器中
- 使用矩阵的分块算法,分块存储矩阵与向量
使用 MapReduce 实现关系运算
- 选择运算
- Map,如果元组 t 满足选择要求 C,则输出 key/value:\((t,t)\) ,只要 key 是 t 就行
- Reduce,没有特殊功能,直接输出 Map 提供的元组 t 即可
- 投影运算,类似于裁剪,只获得每个元组中需要的那些属性值
- Map,将元组 t 中不需要的元素提出得到新元组 t’,Map 返回元组:\((t',t')\)
- Reduce,Map 函数很可能生成很多重复的 Value,Reduce 函数将 \(\left(t^{\prime},\left[t^{\prime}, t^{\prime}, \cdots, t^{7}\right]\right)\) 转换为 \((t',t')\)
- 集合 并/交/差 运算
- 并集相对简单,这里忽略
- 做两个集合的交集之前需先剔除原集合中重复的元素
- Map,将所有输入转化为 \((t,t)\)
- Reduce,如果 key 对应的值表有两个元素则输出当前 key ,否则不输出
- 差集的计算,假设计算集合 R 和 S 之间的差集
- Map,生成 \((t,R)\) 和 \((t,S)\),R 和 S 只用来表明当前元素所处的集合
- Reduce,每个 key ,如果值表中仅有 R,则输出 key,否则不输出
- 集合之间的自然连接 & 分组与聚合运算(略)
使用关系运算实现矩阵乘法(两步法)
矩阵 \(P=MN\) 的计算过程如下:
\[p_{i k}=\sum_{j} m_{i j} n_{j k} \]
实际使用的大型矩阵一般比较稀疏,所以常用关系法保存矩阵:\(M(I,J,V)\) 和 \(N(J, K, W)\),其中 I/J 表示元素在矩阵中的位置,V 是值。使用 MapReduce 计算矩阵之积需要三步,自然连接/分组/聚合:
- 自然连接生成:\((i, j, k, v, w)\) ,J 是矩阵 M 和 N 的关联值,进一步得 \((i, j, k, v \times w)\)
- 分组:以 \((i,k)\) 为 key ,将自然连接到元素合并到一起
- 聚合,将 \(((i,k),[...])\) 中值表元素求和即可得结果矩阵对应元素的值
相似项发现
-
Jaccard 相似度
- 集合的 Jaccard 相似度:\(|S \cap T| /|S \cup T|\)
- 搜索引擎在返回搜索结果时常使用相似度过滤相同的返回项;反抄袭中亦使用相似度检测作弊情况
- bag jaccard,包和集合的区别在于前者剔除了重复数据,后者保留了重复数据
-
协同过滤。使用 Jaccard 描述用户相似度时一般阈值较低,比如 20% 就可认为用户相似;网页的相似度用 jaccard 进行描述时一般阈值设置较高,比如 90%
-
集合的矩阵表示(3.3.1)。集合的矩阵表示一般用于数据可视化而不是存储方式
-
最小 hash (minhashing)
- 注意最小 hash 和 jaccard 相似度的关系:两个集合随机排列转换后最小 hash 相等的概率等于这两个集合的 Jaccard 相似度
-
minhashing 签名:\(\left[h_{1}(\mathrm{~S}), h_{2}(S), \cdots, h_{n}(S)\right]\)
-
minhashing 签名的 hash 函数计算法
- 从理论方法计算 minhashing 签名比较耗时,因为要做大量数据行交换;借用 hash 函数的随机性可以不用交换数据就可以求得每个 hash 函数对应的 minhashing(每一种 hash 对应着一次随机行变换),如下图所示 \(h_n\) 为不同的 hash 函数,\(S_n\) 为不同集合。这里主要使用 hash 函数的随机性,将顺序的行号随机排列,部分冲突并不过于影响签名的特性
\[\begin{array}{ccccc} & S_{1} & S_{2} & S_{3} & S_{4} \\ \hline h_{1} & 1 & 3 & 0 & 1 \\ h_{2} & 0 & 2 & 0 & 0 \end{array} \]
- 从理论方法计算 minhashing 签名比较耗时,因为要做大量数据行交换;借用 hash 函数的随机性可以不用交换数据就可以求得每个 hash 函数对应的 minhashing(每一种 hash 对应着一次随机行变换),如下图所示 \(h_n\) 为不同的 hash 函数,\(S_n\) 为不同集合。这里主要使用 hash 函数的随机性,将顺序的行号随机排列,部分冲突并不过于影响签名的特性
-
局部敏感函数理论(略)
文档 shingling
- 识别相似文档的有效方法是构建文档中短字符串的集合。k-shingle 就是文档中任意长度为 k 的子串
- 如果 k=1,则所有文档的 shingling jaccard 相似度都是很高,因为英文只有 26 个英文字母,且每篇文档都包含绝大部分英文字符。对于邮件,一般 k 选择 5;像论文这样的大文档, k 一般选择 9;空格一般忽略
- 对 shingling 进行 hash 可以减少存储并提高检测速度
- 从信息的角度,很多字符很少见,所以计算 shingling 个数的时候认为文档中有 20 种字符而不是 26 个
相似性度量与常见距离
距离度量的定义:
- \(d(x, y) \geqslant 0\),非负性
- 当且仅当 \(x=y\) 时 \(d(x,y)=0\)
- \(d(x, y)=d(y, x)\),对称性
- \(d(x, y) \leqslant d(x, z)+d(z, y)\),三角不等式。即从 x 到 y 途径某个特定的第三点没有任何好处。三角不等式保证最短距离
常见距离如下:
- 欧式距离:\(d\left(\left[x_{1}, x_{2}, \cdots, x_{n}\right]\right),\left[y_{1}, y_{2}, \cdots, y_{n}\right]=\left(\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|^{r}\right)^{1 / r}\)
- Jaccard 距离,1 减 Jaccard 相似度
- 余弦距离
- 汉明距离,向量中不同分量的个数
- 编辑距离
- 只适合字符串的比较。将字符串 x 转换为字符串 y 所需要的最小字符插入和删除次数
- LCS(longest common subequence),最长公共子序列也可用于编辑距离
LSH
从百万数据集中对比数据,如果使用常规的比较法,那么每次的查询时间复杂度都是 \(O(n)\) ,海量的查询(\(O(n^2)\))将极耗资源,LSH(Locality Sensitive Hashing)利用 hash 方法在存在一定误差的情况下极大的提高了检索效率
利用 LSH 将数据或者签名字符串切分为若干片段,每个片段对应一个 hash 桶,对每段求 hash 并放到指定的桶。对比时直接看桶中是否同时存在对应的数据,如果多个桶中都包含对比数据,说明两个数据很相似
LSH 的缺点:伪反例与伪正例,可以通过配置桶个数与相关阈值来限定相关的概率
LSH 的典型应用有指纹检索/相似文档检索等,LSH 适合对相似度要求不高的匹配场景
高相似度项过滤方法
使用比较法在海量数据中寻找高度相似的项比较耗时,所以一般使用各种手段减小对比项的个数,例如:
- 基于长度的过滤
- 前缀索引 / 位置索引 / 后缀索引
使用这些方法的前提是对集合的元素进行排序
数据流挖掘
- 存储器分类
- 工作存储器,容量有限的内存或者硬盘,可以用来处理查询应答
- 一般的实时流处理不访问二级存储器
- 归档存储器,容量很大,比如磁带等,特点是不能处理应答,或者需要很长时间来处理查询应答
- 工作存储器,容量有限的内存或者硬盘,可以用来处理查询应答
- 流数据实例:视频监控;web 流量;物联网传感器数据监控等
- 流查询分类
- standing query:持续执行,遇到符合要求的数据时给出应答。比如温度监控,一旦达到阈值即报警;比如最高温度提取,不断的处理实时流并保存当前最高温度等等
- ad hoc:即席查询,介于实时与离线之间的一种形式。比如工作存储器会保存一天(一个月)所有的登陆信息,那么使用 ad hoc 方式可以查一天的 UV 或者一个月的 UV
- 流数据的抽样问题(关键词段)
- 从流的角度随机抽取数据并不适合所有的场景
- 可以考虑搜索引擎搜索流下的典型用户重复查询比率问题,全局随机样本获得的结果比真实结果要小
- 代表性样本的获取
- 以数据流元素中某个字段比如用户 ID 为基准随机抽取样本更适合上面的重复查询问题
- 注意 hash 方法在样本抽取中的应用,不使用 hash 方法,实时流抽样几乎不可实现
- 从流的角度随机抽取数据并不适合所有的场景
布隆过滤器
布隆过滤器的冲突概率仅仅和使用当前过滤器的数据集有关。举个曝光过滤的例子:
推荐场景下一般需要曝光服务过滤那些最近一段时间内用户看过的物料。简单的曝光服务可以是记录一段时间内用户看过的物料的 ID 列表,这个列表按照需求,一般需要几个 KB 的存储空间。如果使用布隆过滤器,假设一个用户一月最多看 1000 个物料,使用这个工具 ,一个用户使用 2KB 的存储空间和 6 个 hash 函数就可以实现不高于万分之九点三的曝光误差。使用布隆过滤器相对于普通的列表而言可以大大减少数据在不同机器之间的传输,假设我们使用 redis 存储曝光信息,redis 提供了布隆过滤器相关函数,不需要读出数据即可判断曝光状态。在超高的并发场景下(单机10W QPS),数据的传输是 redis 的主要瓶颈,使用布隆过滤器可以减少数据传输压力
独立元素计数(HLL)
独立元素计数(DV count, Distinct Value)的精确方法一般使用集合,海量数据的快速计算方法一般使用统计方法,比如书中所说的 FM 算法,工程领域常用的方法是 HyperLogLog (HLL),redis 中有 HLL 的实现方法
redis 中默认使用 \(2^{14}=16384\) 个 6bit 单元(\(2^6=64\)),大概 12KB 的存储空间来实现一个 HLL 统计对象
HLL 的简单解释
一个 64 位的二进制整数,左侧有 n 个 0 的情况有 \(2^{63-n}\) 种,各种情况中数据个数占所有数据个数的比例为 0.5/0.25/0.125/0.0625…,即每种情况数的个数是前一种的一半
随着 DV 的增加,左侧更多 0 的二进制数更容易取到,所以下面命题的曲线有全局极大值:
随着 DV 个数的增加,求 64bit hash 值中左侧最多连续 0 个数为 n 的概率
有全局极大值的函数可以通过一定的手段无限放大极值的优越性,最终让极值出现的概率无限趋近于1,其他位置出现的概率趋近于 0 。这就是 HLL 使用很多个 6 bit 单元的原因(一个 6bit 可以记录一种 hash 情况下左侧出现的最多 0 的个数),一个 6bit 单元的误差比较大,但近万个统计单元,根据大数定律,统计结果就很接近真实值了
矩估计
矩对应着向量元素的操作,当大量数据无法全部存储的时候精确的矩计算就比较困难,下面给出 AMS 算法,可以使用少量存储空间估计出数据集二阶及以上阶的值。矩定义如下,其中 \(m_i\) 表示集合去重后第 \(i\) 个元素在整个集合中出现的次数
\[A_{k}=\sum_{i=1}^{n} m_{i}^{k} \]
- k=0,0 阶矩,DV count,HLL
- k=1,1 阶矩,总数据量,使用计数器即可实现
- k=2,2 阶矩,度量数据分布的非均匀性。假设有 10 个元素,如果都重复,则二阶矩的值为10,如果有一个元素出现了 9 次,另一个出现了 1 次,则值为 82
AMS 矩估计
AMS 全称为 Alon-Matias-Szegedy Algorithm
假设 X 为流中某个位置的元素,X.value 为后续流中 X 出现的次数,那么通过可得:
\[E(n \times(2 X.\text {value }-1))=\sum_{a} 1+3+5+\cdots+\left(2 m_{a}-1\right)=\sum_{a}\left(m_{a}\right)^{2} \]
期中 \(m_a\) 表示第 a 个独立元素出现的次数,\(n\) 为流的长度。上式右侧刚好为二阶矩的定义。求解上式的一个重要基础如下:
\[1+3+5+\cdots+\left(2 m_{a}-1\right)=m_{a}^{2} \]
选择不同的公式可以估计流更高阶的矩,例如使用下式可以求流的三阶矩
\[\sum_{v=1}^{m} 3 v^{2}-3 v+1=m^{3} \]
使用 AMS 矩估计需要保证每个位置被选择的概率相同
窗口内的计数问题
假设我们需要查询这样的一个问题:
对于任意的 \(k\le N\),最近 \(k\) 位中有多少个 1?
精确回答上面问题需要记录每一位的值,在大量数据下会消耗海量的存储空间
线段树
在 N 定长的前提下使用线段树可以实现快速的查询,周期性分数据段构建线段树并在合适的时机进行线段树的合并可以实现实时快速查询,但完整的线段树比较耗时且构建过程十分消耗资源,所以可以考虑减小线段树叶子结点的尺度,这样可以减少线段树的大小,但降低了精读
DGIM(Datar-Gionis-Indyk-Motwani)
DGIM 算法能够使用 \(O(log^2N)\) 位来表示大小为 \(N\) 的窗口,同时保证窗口内计数估计错误率不高于 50%
链接分析
PageRank
随机过程一般涉及多个连续的状态,后续的状态一般与前面的若干个状态相关联,马尔可夫过程简化了这个模型,其认为后续过程只与前一个过程相关
初始条件下 PageRank 向量被设置为 n 个值为 1/n 的列向量,每次马尔可夫过程都是使用期望的方式求解用户留在当前页面的概率,其实就是当前页面的 PageRank 值,对于满足马尔可夫过程的图,这个向量终究会收敛
存在终止点的图,随着马尔可夫过程的迭代,用户会陷入终止点,从而造成其他位置的 PageRank 值为 0
马尔可夫过程
使用马尔可夫过程计算 PageRank 的两个前提
- 图的强联通关系
- 图中不存在终止点
假设 web 的转移矩阵如下(4 个 web 页面,每列之和为1,列元素表示其他页面到达当前页面的概率):
\[M=\left[\begin{array}{cccc} 0 & 1 / 2 & 1 & 0 \\ 1 / 3 & 0 & 0 & 1 / 2 \\ 1 / 3 & 0 & 0 & 1 / 2 \\ 1 / 3 & 1 / 2 & 0 & 0 \end{array}\right] \]
将 PageRank 向量初始化为长度为 n 且元素值均为 1/n 的列向量 \(v_0\) ,则这些网页的 PageRank 值可以通过下式计算得出,i 的取值一般在 50~75 之间,下式最终会收敛到一个固定的向量
\[v_i = M^iv_0 \]
非强联通图的修整(剔除/抽税)
使用马尔可夫过程计算 PageRank 的前提有两个,如上文。但现实场景一般不满足这个要求,所以需要使用各种手段使数据达到这两个要求
-
循环剔除终止点
-
抽税法(\(\beta\) 取值一般在 0.8 到 0.9 之间)
\[\mathbf{v}^{\prime}=\beta M \mathbf{v}+(1-\beta) \mathbf{e} / n \]
频繁项集
购物篮模型与智能营销
购物篮模型源自商场购物车,用户每天购买了大量商品,用户每次付款时所购买的物品都可以看作一个购物车里的商品。部分商品有一定的关联性,有些相关性比较明显,比如牛奶/面包;有些则不明显,比如啤酒/尿布。使用相关性可以做一些智能营销,比如做热狗促销的时候提高芥末的价格(商家的一贯套路)
购物篮模型可以扩展到文档比对等领域
关联规则
- 支持度:集合 \(I\) 的支持度是包含 \(I\) 的购物篮个数
- 为了减少计算量,线上商店一般把支持度比例设置为 1%
- 可信度: \(I \rightarrow j \) 的可信度为 \(I\cup\{j\}\) 的支持度与 \(I\) 支持度的比值
- 兴趣度, \(I \rightarrow j \) 的兴趣度为其可信度与保护 \(j\) 的购物篮之间的差值
- 值为 0 表示两者没有相关关系
- 值为正表示前者对后者有一定的促进或者说正相关性,比如买牛奶一般会买面包
- 值为负表示前者对后者有一定的抑制,比如买可口可乐的一般不买百事
A-priori 算法
对于 \(n\) 个项组成的购物篮,大小为 \(k\) 的所有子集生成时间复杂度为 \(n^k/k!\) 。假设 \(k\) 为 2,\(n\) 为 30000,那么所有子集的个数为 4.5 亿个,每个项使用四字节 int 标识,4.5 亿个二元组需要大致 1.67 GB 的存储空间。真实场景下购物篮中项的个数以百万计,即使是 10 万量级的三元组,也需要将近 620TB 的计数存储空间。朴素算法不适合大量量数据的计算
使用 hash 与三角矩阵
频繁项可以用于真实的购物篮,也可以用于文档处理,为了算法的通用性,一般将所有项使用 int 变量进行表示,所以相关算法一般都需要对原始数据进行多次扫描。第一次给所有项标号,一般配合 hash 算法
将所有元素转化为整数后,每个二元组都可以使用二维数组中的一个元素表示,因为组合的原因,如果真的使用二维数组保存数据,那么至少有一半的空间被浪费了,所以可以利用组合的特点,使用一维三角数组中的元素表示二元组,一维数组的下标为:\(k=(i-1)\left(n-\frac{i}{2}\right)+j-i, 1 \leqslant i \leqslant j \leqslant n\)
如果频繁项集相对比较稀疏(比如明显小于总量的 1/3),那么可以使用类似于 map 的方式存储数据
单调性
频繁项集的单调性:如果项集 \(I\) 是频繁的,那么其所有的子集都是频繁的
算法流程
A-priori 基于若干前置条件:
- 单元素项集一般是可以放到内存中的,千万元素转化为 int 后只需要不到 50MB 的内存(10 亿个 int 不超过4GB内存)
- 频繁项个数要远小于全集中项的个数,A-priori 正是利用的这个现行每个流程过滤一部分数据
- 频繁项集的单调性
- 内存大小足够容纳每次计算所需的数据,购物篮有一定的随机性如果计算的过程发生内存换页,将极大降低算法的效率
A-priori 算法分为两个流程:
- 将项使用 int 描述并利用一个数组统计所有项在购物篮中出现的次数(数组的下标对应项转化后的 int 整数,int 整数的分配是顺序的)。设定支持度阈值(比如1%),过滤那些较少出现的项,最后生成频繁项表,频繁项表也是一个数组,但其大小要比全集项使用的数组要小
- 对于每一个购物篮,先使用频繁项表过滤一次。求二元频繁项集,通过一个双重循环即可
A-priori & k 元频繁项集
在知道每个 k 元频繁项集的前提下,可以使用 A-priori 算法求 k+1 元频繁项集,思路和求解二元频繁项集相同,使用前置条件过滤大量无效数据以减少计算量
海量 C2 数据集的处理
这里 C2 表示 A-priori 算法二元组统计过程中的所有二元组,一般而言 C2 是所有频繁项集中数据量最大的
频繁项集一般比较稀疏,即使使用 A-priori 算法第一遍流程剔除了很多不频繁的单项集,二元频繁项依旧比较稀疏,所以可以考虑使用 hash 桶而不是三角数组来对频繁项进行计数。hash 桶虽然不能保证项对的频繁性,但可以过滤那些不频繁的二元项 ,此类算法有 PCY 等多阶段算法
其他算法
- 随机化方法,使用样本而非全集,比如 SON/Toivonen
- 用于流的频繁项统计方法(略)
聚类
维数灾难
使用向量描述物料特征时并不是向量越长越好,过长的向量不但会增加计算复杂度还会降低精度。过长维度造成的问题可以查看此篇文章,例如长维度容易造成过拟合
维数灾难的表现:
-
几乎所有点之间的距离都相等
-
任意向量之间几乎均为正交,以下式为例,归一化后随机点之间的余弦距离在大维度下趋近于 0
\[\frac{\sum_{i=1}^{d} x_{i} y_{i}}{\sqrt{\sum_{i=1}^{d} x_{i}^{2}} \sqrt{\sum_{i=1}^{d} y_{i}^{2}}} \]
聚类策略
聚类策略分为两大类,由底向上的层次算法 & 由上向下的点分配算法
由下向上的层次算法 ,一般适用于少量数据,算法流程就是不断的构建更大的簇
在二维和三维空间中可以使用坐标中心表示一个簇,也有其他形式的簇表示法方法,比如基于半径/Jaccard距离等

由上向下的点分配算法 ,点分配算法会预先假设整个数据集的种类数,比如结合抽样和层次算法获得一个提示;比如计算一个区间内所有聚类结果,使用最优的那个种类数
- 比如 k-means 算法
常见聚类算法
- k-means
- BFR/CURE/GRGPF
- 流聚类 DGIM
Web 广告
广告分类:
- 普通广告
- 个性化广告,比如各 APP 中的推荐广告
- 搜索广告,一般通过搜索竞价实现
广告展示的在线与离线算法
web 广告的优势是可以定制化展示。定制化的前提是使用用户的历史数据计算出用户的偏好
一般而言离线算法的效果要比在线算法要好,但离线算法没有时效性,所以线上依旧使用的是在线算法。离线算法优于在线算法的一个因素是离线算法知道各单词的查询次数,比在线算法知道更多“未来”的信息
竞争率
在线算法比最优的离线算法要差,假设离线算法的最优收益是 \(\alpha\) ,在线算法的收益是 \(\beta\) ,如果存在一个小于 1 的常数 \(c\) 使得 \(\beta = c\cdot \alpha\) 则称 \(c\) 为在线算法的竞争率
贪心算法
web 广告常用贪心算法,最大化搜索引擎与广告主之间的利益
adwords & balance
adwords 问题的定义如下:
- 广告商为搜索设定的投标价格集合
- 每个广告商的预算
- 每个搜索可显示广告数的上限
- 每个广告商-查询对应的广告点击率
已知上述问题,每次搜索时搜索页面会同时给出一个侧边广告栏,因为一次搜索可以展示的广告个数有限,所以算法需要找到最优的广告展示方式。google 一般使用收益最大化作为优化的目标函数
balance 是一个相对比较简单的广告分发算法,具体细节可以看原文
文档匹配与广告分发
- google 会在邮件中携带广告,匹配的是邮件的内容
- twitter 匹配用户发的博文,然后匹配相关的广告
- 在线新闻匹配新闻内容,然后匹配相关广告
- 其他,比如小说中携带广告等等
推荐系统
推荐系统可以按照技术方式分为两大类:
- 基于内容,基于推荐项的性质
- 基于协同过滤,通过计算项和用户之间的相似度来推荐
推荐系统的应用非常广泛,比如商品/书籍/电影/新闻等等
长尾现象
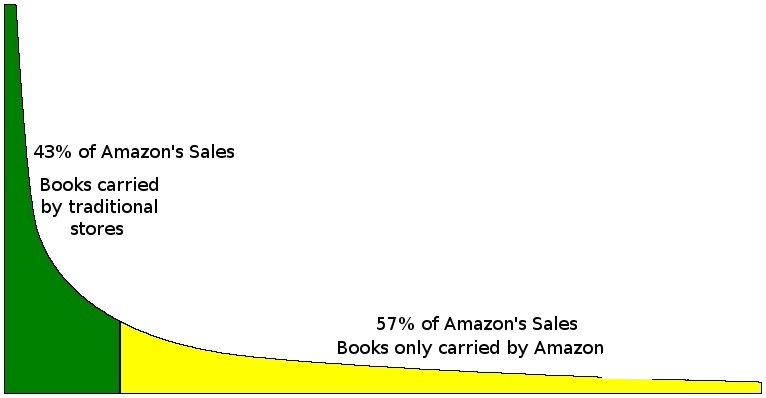
长尾现象是幂律现象的通俗提法。长尾(The Long Tail),或译为长尾效应,是指那些原来不受到重视的销量小但种类多的产品或服务由于总量巨大,累积起来的总收益超过主流产品的现象。比如下图,亚马逊有 43% 的书籍销售源自经典商品,也就是那些关注度比较高的商品;57% 的销售源自那些很少被人关注的书籍,如果没有推荐系统,这些书籍极少会被关注与购买
基于内容的推荐
在基于内容的推荐系统中我们需要为每一个项建立一个模型,用于表示该项的重要特性
电影
比如电影可以有如下特性:
- 演员集合,有些用户喜欢某些演员
- 导演/制作年份/电影流派等等
可以参考 IMDB 查看与电影相关的一些属性
文档
对于文档类型的物料,经常使用高 TF.IDF 得分的单词作为文档的属性描述
基于 tag 的属性描述(略)
提升推荐速度
常规使用超平面和 LSH
矩阵计算时因矩阵的稀疏性,使用矩阵分解以提高效率
协同过滤(略)
社会网络图挖掘
社会网络图有很多种,比如:
- 微信/QQ 朋友圈
- 电话网络/邮件网络
- 合作网络,比如论文作者
- 信息网络/基础网络(道路、管道)/生物网络(基因、蛋白、生物圈等)
社会网络可以用图进行描述
中介度(边介数)
中介度(Betweenness) 描述了节点在其它节点之间的最短路径上出现的次数。次数越多,中介度越高
社会网络一般只有连接关系没有直接的方式度量节点之间的相关性,中介度可以作为节点之间的一种距离,随后就可以使用常规的聚类算法获得节点之间的社区关系
获得网络中各节点的中介度之后依次剔除中介度大的连线依旧可以获得社会网络的社区关系
GN 算法
Girvan-Newman 2002 年提出的社团发现算法(GN 算法清晰明了但复杂度较高),流程如下:
- 计算网络中各条边的中介度
- 可以利用 BFS 求各点之间的最短路径,出现在最短路径上越多的边,其中介度越大。注意两点之间的最短路径不唯一
- 找出中介度最大的边,并将它移除(如果最大边介数的边不唯一,那么既可以随机挑选一条边断开也可以将这些边同时断开)
- 重新计算网络中剩余各条边的中介度
- 重复第 2、3 步,直到网络中所有的边都被移除
GN 算法属于层次聚类算法
“背叛者”
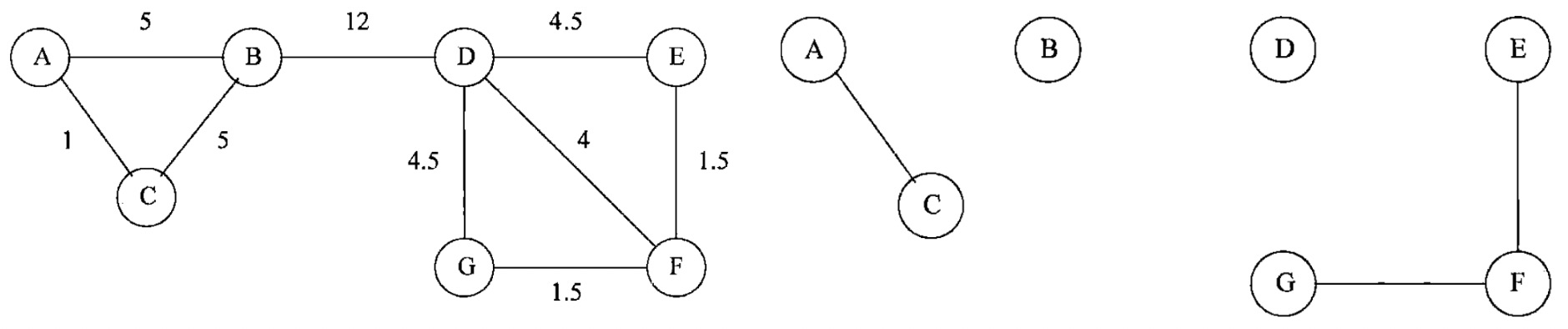
如下图所示,B/D 被单独列为一个社群,可以使用背叛者的概念进行解释,B/D 刚好是两个社群的连接者,有一定的背叛属性
其他部分(暂略)
11 & 12 章 降维处理 & 大规模机器学习
暂略